练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

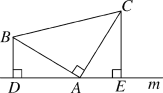
    【题目】如图，已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E.求证：(1)△BDA≌△AEC；(2)DE＝BD＋CE.

    【答案】（1）证明见解析；（2）证明见解析.

    【解析】

    （1）利用已知得出∠CAE=∠ABD，进而利用AAS得出△BDA≌△AEC即可；

    （2）由△BDA≌△AEC，可得出BD=AE，DA=CE，继而利用线段的和差即可得到结论.

    （1）∵BD⊥直线m，CE⊥直线m，

    ∴∠BDA=∠CEA=90°，

    ∵∠BAC=90°，

    ∴∠BAD+∠CAE=∠BAD+∠ABD=90°，

    ∴∠ABD=∠CAE，

    在△ABD和△CAE中

    ，

    ∴△BDA≌△AEC（AAS）；

    （2）∵△BDA≌△AEC，

    ∴BD=AE， DA=CE，

    ∵DE=AD+AE，

    ∴DE= BD+CE.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知⊙O的直径AB=2，弦AC与弦BD交于点E．且OD⊥AC，垂足为点F．

    （1）如图1，如果AC=BD，求弦AC的长；

    （2）如图2，如果E为弦BD的中点，求∠ABD的余切值；

    （3）联结BC、CD、DA，如果BC是⊙O的内接正n边形的一边，CD是⊙O的内接正（n+4）边形的一边，求△ACD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学为了解全校学生到校上学的方式，在全校随机抽取了若干名学生进行问卷调查．问卷给出了五种上学方式供学生选择，每人只能选一项，且不能不选．同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图（均不完整）．请根据图中提供的信息解答下列问题：

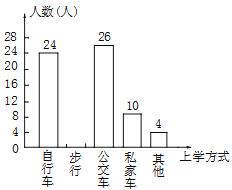
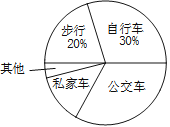
    （1）在这次调查中，一共抽取了多少名学生？

    （2）通过计算补全条形统计图；

    （3）在扇形统计图中，“公交车”部分所对应的圆心角是多少度？

    （4）若全校有1600名学生，估计该校乘坐私家车上学的学生约有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CA⊥BC，垂足为C，AC＝2cm，BC＝6cm，射线BM⊥BQ，垂足为B，动点P从C点出发以1cm/s的速度沿射线CQ运动，点N为射线BM上一动点，满足PN＝AB，随着P点运动而运动，当点P运动_____秒时，△BCA与点P、N、B为顶点的三角形全等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，为锐角，点为直线上一动点，以为直角边且在的右侧作等腰直角三角形，，.

    （1）如果，.

    ①当点在线段上时，如图1，线段、的位置关系为___________，数量关系为_____________

    ②当点在线段的延长线上时，如图2，①中的结论是否仍然成立，请说明理由.

    （2）如图3，如果，，点在线段上运动。探究：当多少度时，？小明通过（1）的探究，猜想时，.他想过点做的垂线，与的延长线相交，构建图2的基本图案，寻找解决此问题的方法。小明的想法对吗？如不对写出你的结论；如对按此方法解决问题并写出理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=∠BFD．

    （1）求证：FD是⊙O的一条切线；

    （2）若AB=10，AC=8，求DF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，C为线段AB上一点，点D为BC的中点，且AB＝18cm，AC＝4CD．

    （1）图中共有　 　条线段；

    （2）求AC的长；

    （3）若点E在直线AB上，且EA＝2cm，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1=∠2，∠A=∠D，说明∠F与∠C相等的理由．

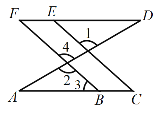
    解：∵∠1=∠2( 已知 )，∠2=∠4 ( )，

    ∴∠1=∠4( 等量代换 )，

    ∴FB∥EC( )，

    ∴∠3=∠C( 两直线平行，同位角相等 )．

    ∵∠A=∠D( )，

    ∴ED∥AC( )，

    ∴∠F=∠3 ( )，

    查看答案和解析>>

    科目：初中数学 来源： 题型：

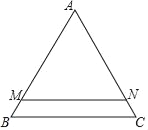
    【题目】如图，△ABC中，AB=AC，∠A=60°，BC=6，直线MN∥BC，且分别交边AB，AC于点M，N，已知直线MN将△ABC分为△AMN和梯形MBCN面积之比为5：1的两部分，如果将线段AM绕着点A旋转，使点M落在边BC上的点D处，那么BD=_____．

    查看答案和解析>>

    同步练习册答案