
【题目】如图,在□ABCD中,对角线 AC、BD 相交成的锐角α=30°,若 AC=8,BD=6,则□ABCD的面积是( )
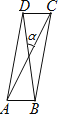
A.6B.8C.10D.12
【答案】D
【解析】
如图,过点D作DE⊥AC于E点,设AC与BD相交于O点,首先根据平行四边形性质得出DO=3,然后利用直角三角形中30°角所对的直角边等于斜边的一半求出DE,由此得出△ACD的面积,最后进一步通过证明△ADC△CBA得出△CBA的面积=△ADC的面积,从而即可得出答案.
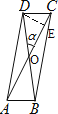
如图,过点D作DE⊥AC于E点,设AC与BD相交于O点,
∵在平行四边形ABCD中,AC=8,BD=6,
∴DO=![]() ,
,
∵∠α=30°,DE⊥AC,
∴DE=![]() ,
,
∴△ACD的面积=![]() ,
,
∵四边形ABCD为平行四边形,
∴CD=AB,AD=BC,
在△ADC与△CBA中,
∵AD=CB,CD=AB,AC=CA,
∴△ADC△CBA(SSS),
∴△CBA的面积=△ADC的面积=6,
∴该平行四边形的面积=△CBA的面积+△ADC的面积=12,
故选:D.


科目:初中数学 来源: 题型:
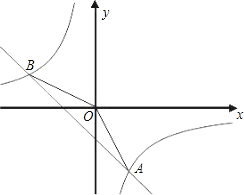
【题目】已知一次函数y= kx+b的图象与反比例函数![]() 的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
(1)求这个一次函数的解析式;
(2)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请求出符合条件的点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是关于x的一元二次方程![]() 的两实数根.
的两实数根.
(1)求m的范围;
(2)若![]() ,求m的值;
,求m的值;
(3)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
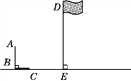
【题目】如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万达旅行社为吸引市民组团去黄山风景区旅游,推出了如下的收费标准:

宿州高铁新区组织员工去黄山风景区旅游,共支付给万达旅行社旅游费用27 000元,请问该单位这次共有多少员工去黄山风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?
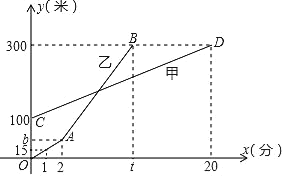
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角形板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。图①,②,③是旋转三角板得到的图形中的3种情况。研究:
(1)三角板ABC绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图②加以证明。
(2)三角板ABC绕点P旋转,△PBE是否能为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。(图④不用)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com