
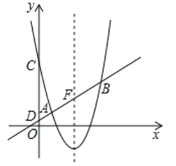
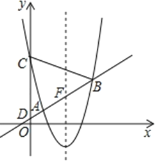
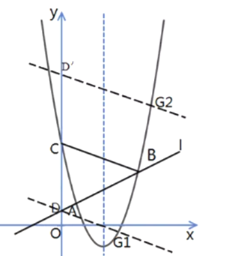
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与直线
与直线![]() 交于A(1,1),B两点,与
交于A(1,1),B两点,与![]() 轴交于点C,直线
轴交于点C,直线![]() 与轴交于点D.
与轴交于点D.
(1)求抛物线的对称轴和点C的坐标;
(2)若在![]() 轴上有且只有一点P,使∠APB=90°,求
轴上有且只有一点P,使∠APB=90°,求![]() 的值;
的值;
(3)设直线![]() 与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若
与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若![]() ,且△BCG与△BCD的面积相等,求点G的坐标.
,且△BCG与△BCD的面积相等,求点G的坐标.
【答案】(1)对称轴是x=2.5 , C的坐标为(0,5);(2)k=![]() ;(3)点G的坐标为(3,-1)或(
;(3)点G的坐标为(3,-1)或(![]() )
)
【解析】
(1)根据对称轴公式即可求出对称轴,根据常数项可得C点坐标;
(2)过点A作AK⊥x轴于点K,过B作BR⊥x轴于点R,设B(p,q),通过△AKP∽△PRB得到q=![]() ,然后根据q=p-5p+5可解得p1=2(舍去),p2=4,然后用待定系数法可求出k的值;
,然后根据q=p-5p+5可解得p1=2(舍去),p2=4,然后用待定系数法可求出k的值;
(3)过点A作AM⊥对称轴于点M,过点B作BN⊥对称轴于点N,构造相似三角形求出B的坐标,从而得到直线AB与直线BD的解析式,求出点D坐标,设点D关于点C的对称点为D′,则 D′(0,![]() ),所以点G在过点D或D′,平行线于BC的直线上,然后联立一次函数与抛物线的解析式即可求出符合题意的点G坐标
),所以点G在过点D或D′,平行线于BC的直线上,然后联立一次函数与抛物线的解析式即可求出符合题意的点G坐标
解:(1)对称轴是x=![]() 2.5
2.5
C的坐标为(0,5)
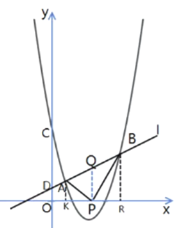
(2)∵在x轴上有且仅有一点P,使∠APB=90,
∴以AB为直径的圆与x轴相切,取AB中点Q,作QP⊥x轴,垂足为P,
过点A作AK⊥x轴于点K,过B作BR⊥x轴于点R,构造“三垂直模型”
设B(p,q),则Q(![]() ,
,![]() ),
),
P(![]() ,0),K(1,0),R(p,0),
,0),K(1,0),R(p,0),
△AKP∽△PRB,AK∶RP=KP∶BR,
∴ 1∶(p-![]() )=(
)=(![]() -1)∶q,
-1)∶q,
化简,得:q=![]() ,
,
∴![]() 2= p-5p+5,
2= p-5p+5,
解得:p1=2,p2=4;
当p=2时,q=![]() <1,k<0,与题中条件k>0矛盾,
<1,k<0,与题中条件k>0矛盾,
∴B(4,![]() ),代入直线l解析式:/p>
),代入直线l解析式:/p>
4k+m=![]() ;
;
又直线l过A(1,1),
∴k+m=1,
联立方程组,解得:k=![]() ;
;
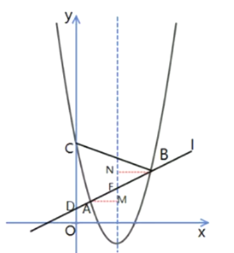
(3)过点A作AM⊥对称轴于点M,过点B作BN⊥对称轴于点N,
∵AF:FB=3:4,∴AM∶BN=3∶4,
∵AM=![]() -1=
-1=![]() ,
,
∴BN=2,即点B的横坐标为2+![]() =
=![]() ;
;
B的纵坐标为:(![]() )-5×
)-5×![]() +5=
+5=![]() ,
,
∴B(![]() ,
,![]() );
);
将A、B坐标代入l解析式:
k+m=1;
![]() +m=
+m=![]() ,
,
解得:k=![]() ,m=
,m=![]() ,
,
∴D(0,![]() );
);
∴直线BC解析式为:![]() +5;
+5;
设点D关于点C的对称点为D′,则 D′(0,![]() ),
),
∵△BCD和△BCG有公共边BC,
∴点G在过点D或D′,平行线于BC的直线上,
分别作DG1∥BC,D′G2∥BC,G1、G2在抛物线上
DG 1解析式:y=![]() +
+![]() ,与y= x-5x+5联立,
,与y= x-5x+5联立,
解得:x1=![]() ,x2=3,
,x2=3,
∵G在对称轴右侧,
∴x=3,y=-1,
∴G1(3,-1);
D′G2解析式:y=![]() +
+![]() ,与y= x-5x+5联立,
,与y= x-5x+5联立,
解得:x1=![]() ,x2=
,x2=![]() (舍去),
(舍去),
∴x=![]() ,y=
,y=![]() ,
,
∴G2(![]() ,
,![]() ),
),
综上所述,点G的坐标为:(3,-1);或(![]() ,
,![]() ),
),


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
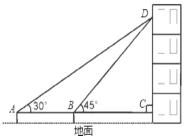
【题目】在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后,又在点B处测得条幅顶端D的仰角为45°,已知测点A.B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度
(计算结果精确到0.1米,参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 阅读材料:如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=900,且点D 在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD。
解决问题:
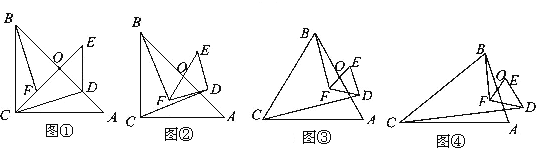
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中结论仍然成立吗?如果成立,请说明理由;如果不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为O,且顶角∠ACB=∠EDF=α,请直接写出![]() 的值(用含α的式子表示出来)。
的值(用含α的式子表示出来)。
查看答案和解析>>
科目:初中数学 来源: 题型:
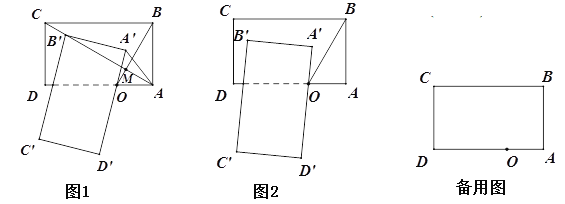
【题目】如图:已知矩形ABCD中,AB=![]() cm,BC=3cm,点O在边AD上,且AO=1cm.将矩形ABCD绕点O逆时针旋转
cm,BC=3cm,点O在边AD上,且AO=1cm.将矩形ABCD绕点O逆时针旋转![]() 角(
角(![]() ),得到矩形A′B′C′D′
),得到矩形A′B′C′D′
(1)求证:AC⊥OB;
(2)如图1, 当B′落在AC上时,求AA′;
(3)如图2,求旋转过程中△CC′D′的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
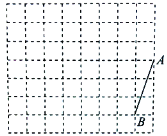
【题目】如图,方格纸中每个小正方形的边长均为1,线段AB的端点均在小正方形的顶点上.
(1)在图中画出以线段AB为一边的矩形ABCD(不是正方形),且点C和点D均在小正方形的顶点上;
(2)在图中画出以线段AB为一腰,底边长为![]() 的等腰三角形ABE,点E在小正方形的顶点,则CE= ;
的等腰三角形ABE,点E在小正方形的顶点,则CE= ;
(3)F是边AD上一动点,则CF+EF的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长城汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润45万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为考察甲、乙两种农作物的长势,研究人员分别抽取了6株苗,测得它们的高度(单位:cm)如下:
甲:98,102,100,100,101,99;乙:100,103,101,97,100,99.
(1)你认为哪种农作物长得高一些?说明理由;
(2)你认为哪种农作物长得更整齐一些?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com