
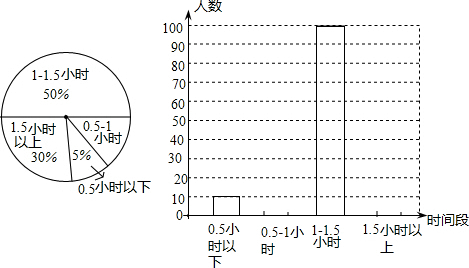
分析 (1)根据统计图中的数据可以求得本次调查的学生数;
(2)根据题意和统计图中的数据可以求得1.5小时以上和0.5~1小时的学生数,从而可以将统计图补充完整;
(3)根据题意和统计图中的数据可以计算出平均每天参加体育活动的时间为“0.5~1小时”部分所对应扇形的圆心角的度数;
(4)根据题意可以计算出全校有多少名学生平均每天参加体育活动的时间不超1小时.
解答 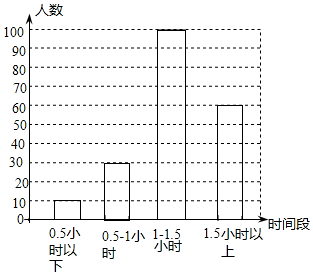 解:(1)由题意可得,
解:(1)由题意可得,
本次一共调查了:10÷5%=200(名),
故答案为:200;
(2)1.5小时以上的有:200×30%=60(名),
0.5~1小时的有:200-10-100-60=30(名),
补全的条形统计图如右图所示;
(3)平均每天参加体育活动的时间为“0.5~1小时”部分所对应扇形的圆心角是:360°×$\frac{30}{200}$=54°,
故答案为:54;
(4)∵3000×$\frac{10+30}{200}$=600,
∴全校有600名学生平均每天参加体育活动的时间不超1小时,
故答案为:600.
点评 本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


科目:初中数学 来源: 题型:选择题
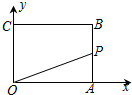 如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A-B-C-O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A-B-C-O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )| A. |  | B. |  | C. | 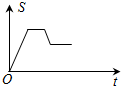 | D. | 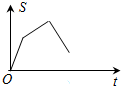 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
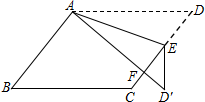 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>3 | B. | k<3 | C. | k>-3 | D. | k<-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
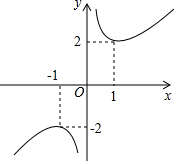 函数y=x+x-1的图象如图所示,下列对该函数性质的论断不可能正确的是( )
函数y=x+x-1的图象如图所示,下列对该函数性质的论断不可能正确的是( )| A. | 该函数的图象是中心对称图形 | |
| B. | 当x>0时,该函数在x=1时取得最小值2 | |
| C. | 在每个象限内,y的值随x值的增大而减小 | |
| D. | y的值不可能为1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
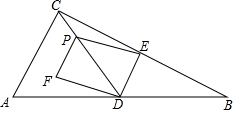 在△ABC中,∠ACB=90°,AC=2$\sqrt{5}$,BC=4$\sqrt{5}$,D、E分别是边AB、BC的中点.点P从点C出发,沿线段CD方向以每秒1个单位长度的速度运动,当点P与点D不重合时,以EP、ED为邻边作平行四边形EDFP.设点P的运动时间为t(t≥0)(秒).
在△ABC中,∠ACB=90°,AC=2$\sqrt{5}$,BC=4$\sqrt{5}$,D、E分别是边AB、BC的中点.点P从点C出发,沿线段CD方向以每秒1个单位长度的速度运动,当点P与点D不重合时,以EP、ED为邻边作平行四边形EDFP.设点P的运动时间为t(t≥0)(秒).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com