
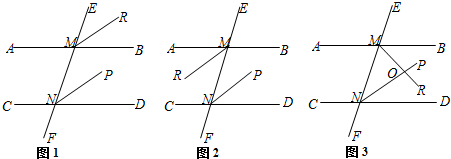
分析 (1)由平行线的性质得出∠EMB=∠END,由角平分线定义得出∠EMR=$\frac{1}{2}$∠EMB,∠MNP=$\frac{1}{2}$∠MND,证出∠EMR=∠MNP,即可得出结论;
(2)由平行线的性质得出∠AMN=∠MND,由角平分线定义得出∠NMR=$\frac{1}{2}$∠EMB,∠MNP=$\frac{1}{2}$∠MND,证出∠NMR=∠MNP,即可得出结论;
(3)由平行线的性质得出∠BMN+∠MND=180°,由角平分线定义得出∠RMN=$\frac{1}{2}$∠BMN,∠MNP=$\frac{1}{2}$∠MND,证出∠RMN+∠MNP=90°,得出∠MON=90°即可.
解答 解:(1)因为AB∥CD(已知)
所以∠EMB=∠END(两直线平行,同位角相等)
因为MR平分∠EMB,NP平分∠MND(已知)
所以∠EMR=$\frac{1}{2}$∠EMB,∠MNP=$\frac{1}{2}$∠MND(角平分线定义)
所以∠EMR=∠MNP
所以MR∥NP(同位角相等,两直线平行)
故答案为:两直线平行,同位角相等;同位角相等,两直线平行;
(2)MR∥NP;理由如下:
因为AB∥CD(已知)
所以∠AMN=∠MND(两直线平行,内错角相等)
因为MR平分∠AMN,NP平分∠MND(已知)
所以∠NMR=$\frac{1}{2}$∠AMN,∠MNP=$\frac{1}{2}$∠MND(角平分线定义)
所以∠NMR=∠MNP
所以MR∥NP(内错角相等,两直线平行)
故答案为:MR∥NP;
(3)MR⊥NP;理由如下:
因为AB∥CD,
所以∠BMN+∠MND=180°,
因为MR平分∠BMN,NP平分∠MND,
所以∠RMN=$\frac{1}{2}$∠BMN,∠MNP=$\frac{1}{2}$∠MND,
所以∠RMN+∠MNP=$\frac{1}{2}$(∠BMN+∠MND)=90°,
所以∠MON=90°,
所以MR⊥NP.
点评 本题考查了平行线的判定与性质、角平分线定义、垂线的证明方法;熟练掌握平行线的判定与性质是解决问题的关键,注意两者的区别.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:解答题
| 等级 | 人数/名 | 百分比 |
| 优秀 | 200 | 20% |
| 良好 | 600 | 60% |
| 及格 | 150 | 15% |
| 不及格 | 50 | a |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
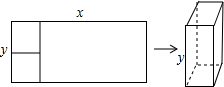 如图,在矩形中截取两个相同的正方形作为长方体的上、下底面,剩余的矩形恰好作为长方体的侧面,设原矩形的长和宽分别为x、y,则y与x的函数图象大致是( )
如图,在矩形中截取两个相同的正方形作为长方体的上、下底面,剩余的矩形恰好作为长方体的侧面,设原矩形的长和宽分别为x、y,则y与x的函数图象大致是( )| A. | 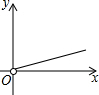 | B. | 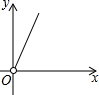 | C. | 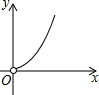 | D. | 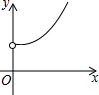 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{18}$ | B. | -$\frac{1}{2}\sqrt{3}$ | C. | $\frac{1}{\sqrt{2}}$ | D. | $\sqrt{\frac{1}{5}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com