
【题目】材料1:反射定律
当入射光线AO照射到平面镜上时,将遵循平面镜反射定律,即反射角(∠BOM)的大小等于入射角(∠AOM)的大小,显然,这两个角的余角也相等,其中法线(OM)与平面镜垂直,并且满足入射光线、反射光线(OB)与法线在同一个平面.
材料2:平行逃逸角
对于某定角∠AOB=α(0°<α<90°),点P为边OB上一点,从点P发出一光线PQ(射线),其角度为∠BPQ=β(0°<β<90°),当光线PQ接触到边OA和OB时会遵循反射定律发生反射,当光线PQ经过n次反射后与边OA或OB平行时,称角为定角α的n阶平行逃逸角,特别地,当光线PQ直接与OA平行时,称角β为定角α的零阶平行逃逸角.
(1)已知∠AOB=α=20°,
①如图1,若PQ∥OA,则∠BPQ= °,即该角为α的零阶平行逃逸角;
②如图2,经过一次反射后的光线P1Q∥OB,此时的∠BPP1为α的平行逃逸角,求∠BPP1的大小;
③若经过两次反射后的光线与OA平行,请补全图形,并直接写出α的二阶平行逃逸角为 °;
(2)根据(1)的结论,归纳猜想对于任意角α(0°<α<90°),其n(n为自然数)阶平行逃逸角β= (用含n和a的代数式表示).

【答案】(1)①20;②∠BPP1=40°③60°;(2)(n+1)α.
【解析】
(1)①两直线平行,同位角相等;②由“反射定律”可得∠AP1Q=∠PP1O,再由P1Q∥OB可得∠AP1Q=∠PP1O=∠AOB=20°;③先作PQ∥AO,再根据“反射定律”先画出P2P1,再画出P1P.
(3)分别从零阶、一阶、二阶逃逸角与∠α的关系中归纳一般性关系.
解:(1)①如图①中,∵PQ∥OA,
∴∠BPQ=∠AOB=20°,
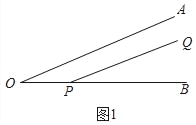
故答案为20.
②如图2中,
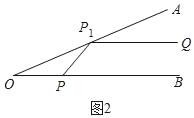
∵P1Q∥OB,
∴∠AP1Q=∠PP1O=∠AOB=20°,
∴∠BPP1=∠AOB+∠PP1O=40°.
③如图3中,如图所示,α的二阶平行逃逸角为20°×3=60°,
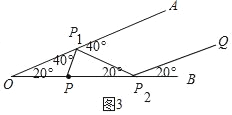
(2)由(1)可知:α的零阶平行逃逸角为α,α的1阶平行逃逸角为2α,α的二阶平行逃逸角为3α,
…,由此可以推出,α的n阶平行逃逸角为(n+1)α,
故答案为(n+1)α.


科目:初中数学 来源: 题型:
【题目】已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO= ![]() ,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.
,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.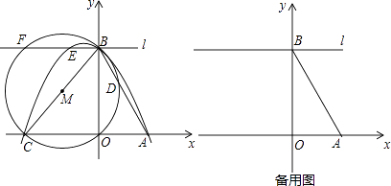
(1)求B点坐标;
(2)用含m的式子表示抛物线的对称轴;
(3)线段EF的长是否为定值?如果是,求出EF的长;如果不是,说明理由.
(4)是否存在点C(m,0),使得BD= ![]() AB?若存在,求出此时m的值;若不存在,说明理由.
AB?若存在,求出此时m的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家、食堂、图书馆依次在同一条直线上,小明从家去食堂吃早餐,接着云图书馆读报,然后回家。如图反映了这个过程,小明离家的距离与时间之间的对应关系,下列说法错误的是( )
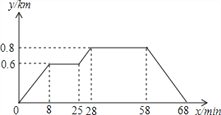
A. 小明从家到食堂用了8min B. 小明家离食堂0.6km,食堂离图书馆0.2km
C. 小明吃早餐用了30min,读报用了17min D. 小明从图书馆回家的平均速度为0.08km/min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y= ![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO= ![]() ,OB=4,OE=2.
,OB=4,OE=2. 
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,延长BC至E使BE=BA,过点B作BD⊥AE于点D,BD与AC交于点F,连接EF.
(1)求证:BF=2AD;
(2)若CE=![]() ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△APB与△CDP均为等边三角形,且PA⊥PD,PA=PD.有下列三个结论:①∠PBC=15°;②AD∥BC;③直线PC与AB垂直.其中正确的有( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李先生购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:米),解答下列问题:
(1)用含x的式子表示客厅的面积;
(2)用含x的式子表示地面总面积;
(3)已知客厅面积比厨房面积多12平方米,若铺1平方米地砖的平均费用为100元,那么铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x(x大于0)秒.
(1)点C表示的数是 ;
(2)当x= 秒时,点P到达点A处?
(3)运动过程中点P表示的数是 (用含字母x的式子表示);
(4)当P,C之间的距离为2个单位长度时,求x的值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com