练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    直线y＝5x＋k与抛物线y＝x2＋3x＋5有一个交点的横坐标为－1，则交点坐标为________．

    答案：(－1，3)，(3，23)
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    直线y＝ax＋c 与抛物线y＝ax2＋bx＋c 在同一坐标系内大致的图象是……（    ）

    （A）      （B）       （C）      （D）

    查看答案和解析>>

    科目：初中数学 来源：2013年河南省平顶山市中考第二次调研测试（二模）数学试卷（带解析） 题型：解答题

    如图，抛物线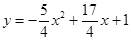与y轴突于A点，过点A的直线y＝kx＋l与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C（3，0）

    （1）求直线AB的函数关系式；
    （2）动点P在线段OC上从原点出发以每秒一个单位的速度向C移动，过点产作PN⊥x轴，交直线AB于点M，交抛物线于点N，设点P移动的时间为t秒，MN的长度为s个单位，求s与t的函数关系式，并求出线段MN的最大值；
    （3）设在（2）的条件下（不考虑点P与点O，点C重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平行四边形？问对于所求的t值，平行四边形BCMN是否菱形？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2013年河南省平顶山市中考第二次调研测试（二模）数学试卷（解析版） 题型：解答题

    如图，抛物线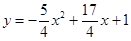与y轴突于A点，过点A的直线y＝kx＋l与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C（3，0）

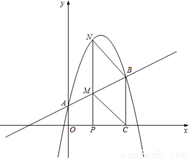
    （1）求直线AB的函数关系式；

    （2）动点P在线段OC上从原点出发以每秒一个单位的速度向C移动，过点产作PN⊥x轴，交直线AB于点M，交抛物线于点N，设点P移动的时间为t秒，MN的长度为s个单位，求s与t的函数关系式，并求出线段MN的最大值；

    （3）设在（2）的条件下（不考虑点P与点O，点C重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平行四边形？问对于所求的t值，平行四边形BCMN是否菱形？请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源：2012届山东省济南市初三模拟考试数学卷 题型：选择题

    （本题满分10分）如图所示，过点F（0，1）的直线y＝kx＋b与抛物线y＝ x2交于M（x1，y1）和N（x2，y2）两点（其中x1＜0，x2＜0）．

    （1）求b的值．

    （2）求x1•x2的值

    （3）分别过M、N作直线l：y＝－1的垂线，垂足分别是M1、N1，判断△M1FN1的形状，并证明你的结论．

    （4） 对于过点F的任意直线MN，是否存在一条定直线m，使m与以MN为直径的圆相切．如果有，请求出这条直线m的解析式；如果没有，请说明理由．

     

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案