
分析 分k=0和k≠0两种情况考虑,当k=0时可以找出方程有一个实数根;当k≠0时,根据方程有实数根结合根的判别式可得出关于m的一元一次不等式,解不等式即可得出k的取值范围.结合上面两者情况即可得出结论.
解答 解:当k=0时,原方程为-4x+1=0,
解得:x=$\frac{1}{4}$,
∴k=0符合题意;
当k≠0时,
∵方程kx2-4x-1=0有实数根,
∴△=(-4)2+4k≥0,
解得:k≥-4且k≠0.
综上可知:k的取值范围是k≥4.
故答案为:k≥4.
点评 本题考查了根的判别式以及解一元一次不等式,解题的关键是分k=0和k≠0来考虑方程有解的情况.本题属于基础题,难度不大,解决该题型题目时,分类讨论是解题的关键.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
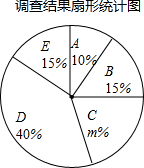 唐诗是我国古代文化中的隗宝,某市教育主管部门为了解本市初中生对唐诗的学习情况,进行了一次唐诗背诵大赛,随机抽取了部分同学的成就(x为整数,总分100分),绘制了如下尚不完整的统计表.
唐诗是我国古代文化中的隗宝,某市教育主管部门为了解本市初中生对唐诗的学习情况,进行了一次唐诗背诵大赛,随机抽取了部分同学的成就(x为整数,总分100分),绘制了如下尚不完整的统计表.| 组别 | 成绩分组(单位:分) | 频数 | 频率 |
| A | 50≤x<60 | 40 | 0.10 |
| B | 60≤x<70 | 60 | c |
| C | 70≤x<80 | a | 0.20 |
| D | 80≤x<90 | 160 | 0.40 |
| E | 90≤x≤100 | 60 | 0.15 |
| 合计 | b | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{120}{x-2}$=$\frac{120}{x}$=-3 | B. | $\frac{120}{x}=\frac{120}{x+2}$-3 | C. | $\frac{120}{x+2}=\frac{120}{x}$-3 | D. | $\frac{120}{x}$=$\frac{120}{x-2}$-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-2$\sqrt{2}$x+2=0 | B. | $\sqrt{{x}^{2}-2}$=-1 | C. | x2-3x+4=0 | D. | 2x2-7x+2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 张浩调查统计了他们家5月份每次打电话的通话时长,并将统计结果进行分组(每组含量最小值,不含最大值),将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )
张浩调查统计了他们家5月份每次打电话的通话时长,并将统计结果进行分组(每组含量最小值,不含最大值),将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )| A. | 张浩家5月份打电话的总频数为80次 | |
| B. | 张浩家5月份每次打电话的通话时长在5-10分钟的频数为15次 | |
| C. | 张浩家5月份每次打电话的通话时长在10-15分钟的频数最多 | |
| D. | 张浩家5月份每次打电话的通话时长在20-25分钟的频率为6% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{11}{x}=\frac{11}{2x}-\frac{1}{3}$ | B. | $\frac{11}{x}=\frac{11}{2x}-20$ | C. | $\frac{11}{x}=\frac{11}{2x}+\frac{1}{3}$ | D. | $\frac{11}{x}=\frac{11}{2x}+20$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com