
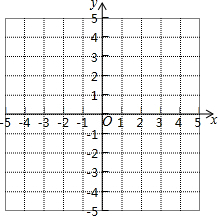
 已知直线y=-2x+4与x轴、y轴分别交于A、D两点,抛物线y=ax2-x+c经过点A、D,点B是抛物线与x轴的另一个交点.
已知直线y=-2x+4与x轴、y轴分别交于A、D两点,抛物线y=ax2-x+c经过点A、D,点B是抛物线与x轴的另一个交点.分析 (1)根据直线解析式可求出A与D的坐标,然后将A、D的坐标代入抛物线的解析式中即可求出a、c的值,然后令y=0代入抛物线的解析式中即可求出B的坐标.
(2)设P(0,m),由(1)可求出点C的坐标,然后根据勾股定理求出BC2、CP2、BP2,由于△BCP为等腰三角形,故分三种情况:BC=CP、BC=BP,BP=CP,然后列出方程求出m的值.
解答 解:(1)令x=0代入y=-2x+4,
∴y=4,
∴D(0,4),
令y=0代入y=-2x+4,
∴x=2,
∴A(2,0),
把A(2,0)和D(0,4)代入y=ax2-x+c,
∴$\left\{\begin{array}{l}{0=4a-2+c}\\{4=c}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=4}\end{array}\right.$
∴抛物线的解析式为:y=-$\frac{1}{2}$x2-x+4
∴令y=0代入y=-$\frac{1}{2}$x2-x+4,
解得:x=2或x=-4
∴B(-4,0)
(2)将C(-2,y)代入y=-$\frac{1}{2}$x2-x+4,
∴y=4,
∴C(-2,4),
设P(0,m)
∵B(-4,0),C(-2,4)
∴由勾股定理可知:BC2=(-4+2)2+(0-4)2=20,
BP2=(-4-0)2+(0-m)2=16+m2,
CP2=(-2-0)2+(4-m)2=4+(4-m)2,
当BC=BP时,
∴BC2=BP2,
∴20=16+m2,
∴m=±2,
P(0,2)或P(0,-2)
若P(0,2)时,此时B、C、P三点共线,
故P(0,-2)
当BC=CP时,
∴BC2=CP2,
∴20=4+(4-m)2
∴m=0或m=-8,
∴P(0,0)或P(0,-8),
当BP=CP时,
∴BP2=CP2,
∴16+m2=4+(4-m)2,
解得:m=$\frac{1}{2}$,
∴P(0,$\frac{1}{2}$),
综上所述,P的坐标为:(0,-2)、(0,0)、(0,-8)、(0,$\frac{1}{2}$)
点评 本题考查二次函数的综合问题,涉及勾股定理,待定系数法求解析式,一元二次方程的解法,等腰三角形的性质与判定,综合程度较高,需要学生综合运用所学的知识.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{m+1}{n}$ | B. | $\frac{m+1}{n+1}$ | C. | $\frac{m}{n+m}$ | D. | $\frac{m-n}{n-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
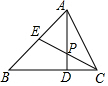 如图,△ABC中,AD⊥BC于点D,CE平分∠ACB交AD于点P,交AB于点E,若∠ABC=45°,∠APE=55°,则∠BAC的度数是65°.
如图,△ABC中,AD⊥BC于点D,CE平分∠ACB交AD于点P,交AB于点E,若∠ABC=45°,∠APE=55°,则∠BAC的度数是65°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲仓库 | 乙仓库 | |
| A工地 | x | 70-x |
| B工地 | 100-x | x+10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
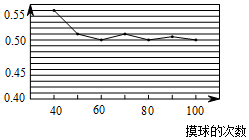 在一个不透明的盒子里装着只有颜色不同的黑、白两种球共30个,小鲍做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是“摸到白色球”的概率折线统计图.
在一个不透明的盒子里装着只有颜色不同的黑、白两种球共30个,小鲍做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是“摸到白色球”的概率折线统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,在Rt△ABC中,AC=6,BC=8,D边AB上一点,连接CD,过点D作DE⊥DC交BC于E,把△BDE沿DE翻折得△DEB1,连接B1C.
已知,如图,在Rt△ABC中,AC=6,BC=8,D边AB上一点,连接CD,过点D作DE⊥DC交BC于E,把△BDE沿DE翻折得△DEB1,连接B1C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com