
阅读下面材料:
定义:与圆的所有切线和割线都有公共点的几何图形叫做这个圆的关联图形.
问题:⊙O的半径为1,画一个⊙O的关联图形.

 |
 个问题时,小明以O为原点建立平面直角坐标系xOy进行探究,他发现能画出很多⊙O的关联图形,例如:⊙O本身和图1中的△ABC(它们都是封闭的图形),以及图2中以O为圆心的 (它是非封闭的图形),它们都是⊙O的
个问题时,小明以O为原点建立平面直角坐标系xOy进行探究,他发现能画出很多⊙O的关联图形,例如:⊙O本身和图1中的△ABC(它们都是封闭的图形),以及图2中以O为圆心的 (它是非封闭的图形),它们都是⊙O的 关联图形.而图2中以P,Q为端点的
关联图形.而图2中以P,Q为端点的 一条曲线就不是⊙O的关联图形.
一条曲线就不是⊙O的关联图形. 参考小明的发现,解决问题:
(1)在下列几何图形中,⊙O的关联图形是 (填序号);
① ⊙O的外切正多边形
② ⊙O的内接正多边形
③ ⊙O的一个半径大于1的同心圆
 (2)若图形G是⊙O的关联图形,并且它是封闭的,则图形G的周长的最小值是____;
(2)若图形G是⊙O的关联图形,并且它是封闭的,则图形G的周长的最小值是____;
(3)在图2中,当⊙O的关联图形 的弧长最小时,经过D,E两点的直线为y =__;
(4 )请你在备用图中画出一个⊙O的关联图形,所画图形的长度l小于(2)中图形G的周长的最小值,并写出l的值(直接画出图形,不写作法).
)请你在备用图中画出一个⊙O的关联图形,所画图形的长度l小于(2)中图形G的周长的最小值,并写出l的值(直接画出图形,不写作法).
科目:初中数学 来源: 题型:
如图,将一张矩形纸片沿对角线剪开得到两个直角三角形纸片,将这两个直角三角形纸片通过图形变换构成以下四个图形,这四个图形中是中心对 称图形的是( )
称图形的是( )
 |
A B C D
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y1=ax2+bx-3的图象经过点A(2,-3),B(-1,0),与y轴交于点C,与x轴另一交点交于点D.
(1)求二次函数的解析式;
(2)求点C、点D的坐标;
(3)若一条直线y2,经过C、D两点,请直接写出y1>y2时,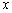 的取值范围.
的取值范围.

x k b
1 . c o m
查看答案和解析>>
科目:初中数学 来源: 题型:
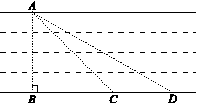
如图,为了估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BD,∠ACB=45°,∠ADB=30°,并且点B,C,D在同一条直线上.若测得CD=30米,求河宽AB(结果精确到1米,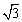 取1.73,
取1.73,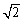 取1.41).
取1.41).
查看答案和解析>>
科目:初中数学 来源: 题型:
如图(1),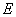 为矩形
为矩形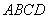 边
边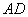 上一点,点
上一点,点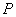 从点
从点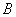 沿折线
沿折线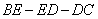 运动到点
运动到点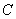 时停止,点
时停止,点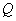 从点
从点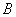 沿
沿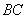 运动到点
运动到点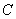 时停止,它们运动的速度都是
时停止,它们运动的速度都是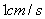 .如果点
.如果点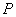 、
、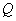 同时开始运动,设运动时间为
同时开始运动,设运动时间为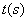 ,
,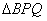 的面积为
的面积为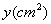 ,已知
,已知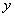 与
与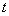 的函数关系的图象如图(2)所示,那么下列结论正确的是( )
的函数关系的图象如图(2)所示,那么下列结论正确的是( )
A. 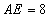 B.
B. 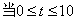 时,
时,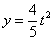
C. 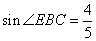
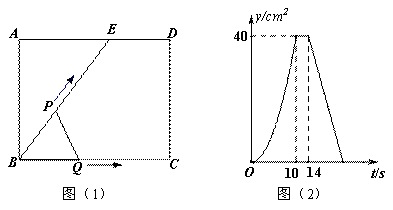 D. 当
D. 当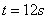 时,
时,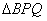 是等腰三角形
是等腰三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com