
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,已知两车相遇时快车比慢车多行驶40千米,快车到达乙地时,慢车还有( )千米到达甲地.

A. 70 B. 80 C. 90 D. 100
【答案】A
【解析】分析:求出相遇前y与x的关系式,确定出甲乙两地的距离,进而求出两车的速度,即可确定出所求.
详解:设第一段折线解析式为y=kx+b,
把(1.5,70)与(2,0)代入得:![]()
解得:![]() 即y=140x+280,
即y=140x+280,
令x=0,得到y=280,即甲乙两对相距280千米,
设两车相遇时,乙行驶了x千米,则甲行驶了(x+40)千米,
根据题意得:x+x+40=280,
解得:x=120,即两车相遇时,乙行驶了120千米,则甲行驶了160千米,
∴甲车的速度为80千米/时,乙车速度为60千米/时,
根据题意得:(280160)÷80=1.5(小时),1.5×60=90(千米),28012090=70(千米),
则快车到达乙地时,慢车还有70千米到达甲地.
故选A.


科目:初中数学 来源: 题型:
【题目】某班组织班团活动,班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品,已知笔记本2元/本,中性笔1元/支,且每种奖品至少买1件.
(1)若设购买笔记本x本,中性笔y支,写出y与x之间的关系式;
(2)有多少种购买方案?请列举所有可能的结果;
(3)从上述方案中任选一种方案购买,求买到的中性笔与笔记本数量相等的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数 y=![]() (a为常数)的图象上有三点(﹣4,y1),(﹣1,y2),(2,y3),则函数值y1 , y2 , y3的大小关系是( )
(a为常数)的图象上有三点(﹣4,y1),(﹣1,y2),(2,y3),则函数值y1 , y2 , y3的大小关系是( )
A.y3<y1<y2
B.y3<y2<y1
C.y1<y2<y3
D.y2<y3<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:
①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE ,
其中正确结论有( )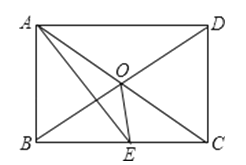
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断正确的是( )
A. 有理数就是正数和负数 B. 没有最小的有理数
C. 任何两个有理数一定可以进行加减乘除运算 D. 在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中,负数共有
中,负数共有![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.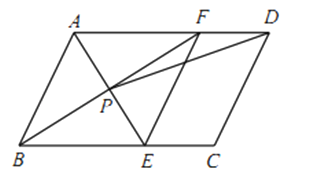
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的集合内:
100,﹣0.82,﹣30![]() ,3.14,﹣2,0,﹣2011,﹣3.1
,3.14,﹣2,0,﹣2011,﹣3.1![]() ,
,![]() ,﹣
,﹣![]() ,2.010010001…,
,2.010010001…,
正分数集合:{ …}
整数集合:{ …}
负有理数集合:{ …}
非正整数集合;{ …}
无理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
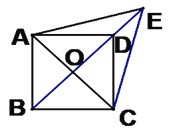
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com