
【题目】桐城市发起了“保护龙眠河”行动,某学校七年级两个班的115名学生积极参与,踊跃捐款,已知甲班有![]() 的学生每人捐了10元,乙班有
的学生每人捐了10元,乙班有![]() 的学生每人捐了10元,两个班其余学生每人捐了5元,设甲班有学生x人。
的学生每人捐了10元,两个班其余学生每人捐了5元,设甲班有学生x人。
(1)用含x的代数式表示乙班人数: ;
(2)用含x的代数式表示两班捐款的总额;
(3)若x=60,则两班共捐款多少元?
【答案】(1)115-x;(2)(-![]() x+805)元;(3)785元.
x+805)元;(3)785元.
【解析】
(1)根据题意可以用含x的代数式表示出乙班的人数;
(2)根据题意可以用含x的代数式表示两班捐款的总额;
(3)将x=60代入(2)中的代数式即可解答本题.
(1)由题意可得,
乙班人数为:115-x,
故答案为:115-x;
(2)![]() x×10+
x×10+![]() (115-x)×10+(1-
(115-x)×10+(1-![]() )x×5+(1-
)x×5+(1-![]() )(115-x)×5
)(115-x)×5
=![]() x+460-4x+
x+460-4x+![]() x+345-3x
x+345-3x
=-![]() x+805,
x+805,
即两班捐款的总额是(-![]() x+805)元;
x+805)元;
(3)当x=60时,
-![]() x+805=-
x+805=-![]() ×60+805=-20+805=785(元),
×60+805=-20+805=785(元),
答:x=60时,两班共捐款785元.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,以下各图都是由同样大小的图形①按一定规律组成,其中第①个图形中共有1个完整菱形,第②个图形中共有5个完整菱形,第③个图形中共有13个完整菱形,…,则第⑦个图形中完整菱形的个数为( )

A. 83B. 84C. 85D. 86
查看答案和解析>>
科目:初中数学 来源: 题型:
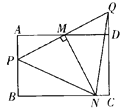
【题目】在矩形ABCD中,AB=8,AD=12,M是AD边的中点,P是AB边上的一个动点(不与A、B重合),PM的延长线交射线CD于Q点,MN⊥PQ交射线BC于N点。
(1)若点N在BC之间时,如图:
①求证:∠NPQ=∠PQN;
②请问![]() 是否为定值?若是定值,求出该定值;若不是,请举反例说明;
是否为定值?若是定值,求出该定值;若不是,请举反例说明;
(2)当△PBN与△NCQ的面积相等时,求AP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-![]() )2 016×161 008;
)2 016×161 008;
【答案】(1)﹣10m2n3+8m3n2;(2)2x﹣40;(3)1.
【解析】试题分析:(1)原式利用单项式乘以多项式法则计算即可得到结果;
(2)原式两项利用多项式乘以多项式法则计算,去括号合并即可得到结果;
(3)先根据幂的乘方的逆运算,把(-![]() )2 016化为(
)2 016化为(![]() )1008,再根据积的乘方的逆运算计算即可.
)1008,再根据积的乘方的逆运算计算即可.
试题解析:(1)原式=(5mn2)(﹣2mn)+(﹣4m2n)(﹣2mn)=﹣10m2n3+8m3n2;
(2)原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40.
(3)原式=(![]() )1008×161 008=(
)1008×161 008=(![]() ×16)1 008=1.
×16)1 008=1.
【题型】解答题
【结束】
19
【题目】如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
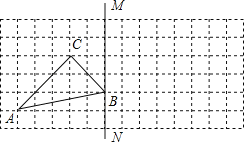
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
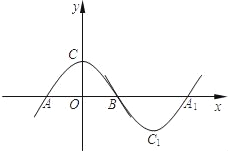
A. ab=﹣2 B. ab=﹣3 C. ab=﹣4 D. ab=﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读思考:
数学课上老师出了一道分式化简求值题目.
题目: ![]() ÷(x+1)·
÷(x+1)·![]() -
-![]() ,其中x=-
,其中x=-![]() .
.
“勤奋”小组的杨明同学展示了他的解法:
解:原式=![]() -
-![]() .........................................................................第一步
.........................................................................第一步
=![]() -
- ..........................................................................第二步
..........................................................................第二步
=![]() ...........................................................................................第三步
...........................................................................................第三步
=![]() ..................................................................................................第四步
..................................................................................................第四步
当x=-![]() 时,原式=
时,原式= .................................................................第五步
.................................................................第五步
请你认真阅读上述解题过程,并回答问题:
你认为该同学的解法正确吗?如有错误,请指出错误在第几步,并写出完整、正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
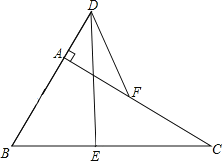
【题目】如图,在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使2AD=AB.连接DE,DF.
(1)求证:AF与DE互相平分;
(2)若BC=4,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com