
 ����x��ĸ�������ÿ��1����λ�ij���ƽ�ƣ�����ƽ�ƹ����и�ֱ�߱���ABCD�صõ��߶γ���Ϊm��ƽ��ʱ��Ϊt��m��t�ĺ���ͼ����ͼ����ʾ��
����x��ĸ�������ÿ��1����λ�ij���ƽ�ƣ�����ƽ�ƹ����и�ֱ�߱���ABCD�صõ��߶γ���Ϊm��ƽ��ʱ��Ϊt��m��t�ĺ���ͼ����ͼ����ʾ��
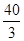 ,��3��
,��3�� ����4��
����4��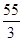 .
.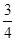 x-6=0�����x=8��
x-6=0�����x=8��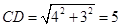 ��
��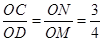 ��
��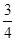 ��x+t��-6��
��x+t��-6��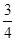 ��0+t��-6=4��
��0+t��-6=4��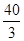 ��
��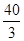 ��
��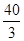 ��4����
��4����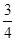 ��-5+t��-6=4��
��-5+t��-6=4��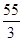 ��
��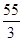 ��0��
��0��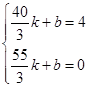 ��
��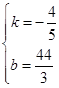 ��
�� ��
��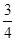 ��-1+t��-6=2��
��-1+t��-6=2��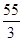 ��
��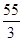 ʱ����ֱ��ƽ��?ABCD�������
ʱ����ֱ��ƽ��?ABCD�������


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
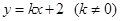 �뷴��������G1:
�뷴��������G1: ��ͼ���ڵ�
��ͼ���ڵ� ��B��b��-1������y�ύ�ڵ�D��
��B��b��-1������y�ύ�ڵ�D�� ��
�� ��ֱ��д��t��ȡֵ��Χ��
��ֱ��д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ���ı���ABCD�ֳ������ȵ������֣���m��ֵΪ ��
���ı���ABCD�ֳ������ȵ������֣���m��ֵΪ ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��1��m��7 | B��3��m��4 | C��m��1 | D��m��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ������
������ ��
�� ������ACB=30�㣬AB=2��
������ACB=30�㣬AB=2�� =x���ı���
=x���ı��� �����ΪS.
�����ΪS. �ij�����Сֵ��_____����ʱx=" _____"
�ij�����Сֵ��_____����ʱx=" _____"  �����Σ���˵�����ɣ�
�����Σ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ����A1����Ϊ(0��1)������A1��y��Ĵ��߽�ֱ��l�ڵ�B1����ԭ��O ΪԲ�ģ�OB1��Ϊ�뾶������yһ���ڵ�A2���ٹ���A2��y��Ĵ��߽�ֱ���ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������y���ڵ�A3��������������������ȥ����A4������Ϊ(_______��_______)����An������Ϊ(_______��_______)��
����A1����Ϊ(0��1)������A1��y��Ĵ��߽�ֱ��l�ڵ�B1����ԭ��O ΪԲ�ģ�OB1��Ϊ�뾶������yһ���ڵ�A2���ٹ���A2��y��Ĵ��߽�ֱ���ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������y���ڵ�A3��������������������ȥ����A4������Ϊ(_______��_______)����An������Ϊ(_______��_______)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ��ֱ��
��ֱ�� ����x��ȡһֵʱ��x��Ӧ�ĺ���ֵ�ֱ�Ϊy1��y2����y1��y2��ȡy1��y2�еĽ�Сֵ��ΪM����y1=y2����M=y1=y2�����磺��x=1ʱ��y1=0��y2=4��y1��y2����ʱM=0��
����x��ȡһֵʱ��x��Ӧ�ĺ���ֵ�ֱ�Ϊy1��y2����y1��y2��ȡy1��y2�еĽ�Сֵ��ΪM����y1=y2����M=y1=y2�����磺��x=1ʱ��y1=0��y2=4��y1��y2����ʱM=0��
 ��
�� .
.| A��1�� | B��2�� | C��3�� | D��4�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com