
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O. 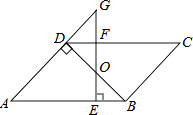
(1)求证:EO=FO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
【答案】
(1)证明:∵四边形ABCD是平行四边形,

∴DC∥AB,
∴∠OBE=∠ODF.
在△OBE与△ODF中,

∴△OBE≌△ODF(AAS).
∴EO=FO;
(2)解:∵EF⊥AB,AB∥DC,
∴∠GEA=∠GFD=90°.
∵∠A=45°,
∴∠G=∠A=45°.
∴AE=GE
∵BD⊥AD,
∴∠ADB=∠GDO=90°.
∴∠GOD=∠G=45°.
∴DG=DO,
∴OF=FG=1,
由(1)可知,OE=OF=1,
∴GE=OE+OF+FG=3,
∴AE=3.
【解析】(1)由平行四边形的性质和AAS证明△OBE≌△ODF,得出对应边相等即可;(2)先证出AE=GE,再证明DG=DO,得出OF=FG=1,即可得出结果.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


科目:初中数学 来源: 题型:
【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,y甲、y乙与x之间的函数图象如图所示. 
(1)甲的速度是km/h;
(2)当1≤x≤5时,求y乙关于x的函数解析式;
(3)当乙与A地相距240km时,甲与A地相距km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(a-b+3)(a+b-3)=( )
A. a2+b2-9 B. a2-b2-6b-9 C. a2-b2+6b-9 D. a2+b2-2ab+6a+6b+9
查看答案和解析>>
科目:初中数学 来源: 题型:
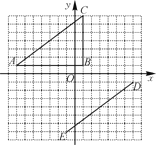
【题目】在平面直角坐标系中,△ABC的顶点坐标是A(-7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,-1),E(-1,-7).
(1)试说明如何平移线段AC,使其与线段ED重合;
(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°.画出旋转后的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线m:y=ax2﹣6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=﹣![]() x+
x+![]() 与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).

(1)求抛物线m的解析式;
(2)P是l上的一个动点,若以B,E,P为顶点的三角形的周长最小,求点P的坐标;
(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com