
����Ŀ����ͼ��AD����O��ֱ����
��1����ͼ1����ֱ��AD��������B1C1��B2C2��Բ��4�ȷ֣�����B1�Ķ����� ����B2�Ķ����� ��
��2����ͼ2����ֱ��AD��������B1C1��B2C2��B3C3��Բ��6�ȷ֣�����B3�Ķ����� ��
��3����ͼ3����ֱ��AD��n����B1C1��B2C2��B3 C3������BnCn��Բ��2n�ȷ֣�����Bn�Ķ����� ���ú�n�Ĵ���ʽ��ʾ��Bn�Ķ�������

���𰸡���1��22.5����67.5������2��75������3��90�㩁![]() ��
��
��������
�����������1�����ÿ�����Ķ�������������Բ�ܽ����ԵĻ��Ķ�����������Բ�ܽǶ�����Բ�ܽǵĶ������������ԵĻ��Ķ�����һ�룩�ó����ɣ�
��2�����ÿ�����Ķ�������������Բ�ܽ����ԵĻ��Ķ�����������Բ�ܽǶ�����Բ�ܽǵĶ������������ԵĻ��Ķ�����һ�룩�ó����ɣ�
��3�����ÿ�����Ķ�������������Բ�ܽ����ԵĻ��Ķ�����������Բ�ܽǶ�����Բ�ܽǵĶ������������ԵĻ��Ķ�����һ�룩�ó����ɣ�
�⣺��1������ֱ��AD��������B1C1��B2C2��Բ��4�ȷ֣�
����B1C1����C1C2����B2C2����B1B2�Ķ�������90������AB1=��AC1��
����AC1�Ķ�����45����
���B1=![]() ��45��=22.5����
��45��=22.5����
��B2=![]() ����45��+90����=67.5����
����45��+90����=67.5����
�ʴ�Ϊ��22.5����67.5����
��2������ֱ��AD��������B1C1��B2C2��B3C3��Բ��6�ȷ�
����B1C1����C1C2����C2C3�Ķ�������60������AB1=��AC1��
����AC1�Ķ�����30����
���B3=![]() ����30��+60��+60����=75����
����30��+60��+60����=75����
�ʴ�Ϊ��75����
��3������ֱ��AD��n����B1C1��B2C2��B3 C3������BnCn��Բ��2n�ȷ֣�
����B1C1����C1C2����C2C3�����Ķ������ǣ�![]() ����=��
����=��![]() ��������AB1=��AC1��
��������AB1=��AC1��
����AC1�Ķ����ǣ�![]() ������
������
���Bn=![]() ����
����![]() +
+![]() +
+![]() +��+
+��+![]() ��=
��=![]() ��[
��[![]() +
+![]() ]��=90�㩁
]��=90�㩁![]()
�ʴ�Ϊ��90�㩁![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����п�չ�������Թ�������ͬ�С����ijУ����ѧ������˫�����ڡ��������μ������Ͷ���Ϊ�˽�ͬѧ���Ͷ������ѧУ��������˲���ͬѧ���Ͷ�ʱ�䣬���õõ������ݻ����˲�������ͳ��ͼ������ͼ����Ϣ�ش��������⣺

��1��������ͳ��ͼ����������
��2������ͼ�еġ�1.5Сʱ������Բ�Ľ��Ƕ��ٶȣ�
��3�������ѧ���Ͷ�ʱ�����������λ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪���κ���![]() ��ͼ����ͼ�������ͼ��ֱ��д���ö��κ���ͼ������������ƽ�ƣ���ͼ��ͨ������ԭ�㣿
��ͼ����ͼ�������ͼ��ֱ��д���ö��κ���ͼ������������ƽ�ƣ���ͼ��ͨ������ԭ�㣿
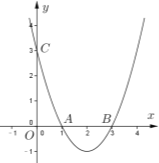
��2���ڹ��ڶ��κ���ͼ����о��У�����ͬѧ����������![]() ��
��![]() ����������
����������![]() ��
��![]() ������
������![]() ��Գƣ�����Э����������ͬѧ���䷢�ֿھ�����
��Գƣ�����Э����������ͬѧ���䷢�ֿھ�����![]() ��
��![]() ���䣬
���䣬![]() �෴������ҷ����������Ա߲��ʼǵĺ�ׯ��ͬѧ��������
�෴������ҷ����������Ա߲��ʼǵĺ�ׯ��ͬѧ��������![]() ��
��![]() �෴��
�෴��![]() �������������˷���д��Ȼ��������д��������ǡ����ԭ������Ҳ�Գƣ�����д��С��ͬѧ��д����ԭ������
�������������˷���д��Ȼ��������д��������ǡ����ԭ������Ҳ�Գƣ�����д��С��ͬѧ��д����ԭ������![]() �ĶԳ�ͼ�εĽ���ʽ�����о�����ԭ�����ߵľ���Գ������
�ĶԳ�ͼ�εĽ���ʽ�����о�����ԭ�����ߵľ���Գ������
��3��������![]() ��
��![]() ������ҽ���
������ҽ���![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ����Գ�����һ�㣬��
����Գ�����һ�㣬��![]() ��
��![]() ���ϣ�����
���ϣ�����![]() �����������������Ե�
�����������������Ե�![]() ��
��![]() ��
��![]() ���������������
Ϊ���������������![]() �п������ƣ���д���������������ĵ�
�п������ƣ���д���������������ĵ�![]() �����ꣻ
�����ꣻ
��4��![]() ��
��![]() ������
Ϊ������![]() �����㣬��
�����㣬��![]() ��
��![]() ����
����![]() �Գƣ���ֱ��д��
�Գƣ���ֱ��д��![]() ��
��![]() ��������ꣻ
��������ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������εij��ȿ���3 cm,��������ij��Ϳ��ֱ�����2 cm���������14 cm2,��ԭ�����ο�Ϊx cm,�������з���ӦΪ�� ��
A. (x+3)(x+2)��x2=14 B. (x+2)(x+5)��x2=14
C. (x+2)(x+5)��x(x+3)=14 D. x(x+2)=14
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴Ӽס�������ͬѧ��ѡ��һ���μӱ����������ǵ����ˮƽ�����˲��飬��������ͬ�����¸����10�Σ����еĻ������£���λ������
�ף�7��8��6��8��6��5��9��10��7��4
�ң�9��5��7��8��6��8��7��6��7��7
��1����![]() ����
����![]() ����S��2��S��2��
����S��2��S��2��
��2������Ϊ��ѡ������ͬѧ�μ����������Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��1022����2��![]() ����3����3x2��2����4y3���£�6xy��2 ��
����3����3x2��2����4y3���£�6xy��2 ��
��4����2a+b��4����2a+b+4������5��a2��a+b����a-b��+a2b2 ����6����2����0+��![]() ����2+����
����2+����![]() ��2016��22017
��2016��22017
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=6����BAC=30������E��CD���ϣ�

��1����AE=4��������ABCE�������
��2������F��AC�ϣ�����BFA=��CEA����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���BAD��ƽ���߽�BC�ڵ�E��OΪ�Խ���AC��BD�Ľ��㣬�ҡ�CAE=15�� .
��1����֤����AOBΪ�ȱ������Σ�
��2�����BOE������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪DC��FP����1����2����FED��28����AGF��80��FHƽ�֡�EFG��
(1)˵����DC��AB��
(2)���PFH�Ķ�����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com