
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.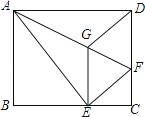
(1)求证:四边形EFDG是菱形;
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2 ![]() ,求BE的长.
,求BE的长.
【答案】
(1)
证明:
∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF.
∴四边形EFDG为菱形
(2)
解:EG2= ![]() GFAF.
GFAF.
理由:如图1所示:连接DE,交AF于点O.
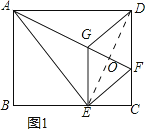
∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF= ![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴ ![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO= ![]() GF,DF=EG,
GF,DF=EG,
∴EG2= ![]() GFAF
GFAF
(3)
解:如图2所示:过点G作GH⊥DC,垂足为H.
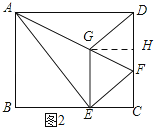
∵EG2= ![]() GFAF,AG=6,EG=2
GFAF,AG=6,EG=2 ![]() ,
,
∴20= ![]() FG(FG+6),整理得:FG2+6FG﹣40=0.
FG(FG+6),整理得:FG2+6FG﹣40=0.
解得:FG=4,FG=﹣10(舍去).
∵DF=GE=2 ![]() ,AF=10,
,AF=10,
∴AD= ![]() =4
=4 ![]() .
.
∵GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴ ![]() ,即
,即 ![]() =
= ![]() .
.
∴GH= ![]() .
.
∴BE=AD﹣GH=4 ![]() ﹣
﹣ ![]() =
= ![]()
【解析】(1)先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF;(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF= ![]() GF,接下来,证明本题主要考查的是四边形与三角形的综合应用,解答本题主要应用了矩形的性质、菱形的判定和性质、相似三角形的性质和判定、勾股定理的应用,利用相似三角形的性质得到DF2=FOAF是解题答问题(2)的关键,依据相似三角形的性质求得GH的长是解答问题(3)的关键.△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系;(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FG∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD﹣GH求解即可.
GF,接下来,证明本题主要考查的是四边形与三角形的综合应用,解答本题主要应用了矩形的性质、菱形的判定和性质、相似三角形的性质和判定、勾股定理的应用,利用相似三角形的性质得到DF2=FOAF是解题答问题(2)的关键,依据相似三角形的性质求得GH的长是解答问题(3)的关键.△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系;(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FG∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD﹣GH求解即可.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
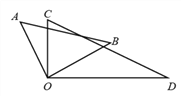
【题目】如图,将一副三角尺的直角顶点重合在一起.
(1)若 OB 是∠DOC 的角平分线,求∠AOD 的补角的度数是多少?
(2)若 ∠COB 与 ∠DOA 的比是 2:7,求 ∠BOC 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒
点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒![]() 过点D作
过点D作![]() 于点F,连接DE、EF.
于点F,连接DE、EF.
![]() 求证:
求证:![]() ;
;
![]() 四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
![]() 当t为何值时,
当t为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数 1,3,5,7,9,…,排成如图的数阵.
(1)十字框中的五个数的和与中间数 15 有什么关系?
(2)设中间数为 a,用式子表示十字框中五个数之和;
(3)十字框中五个数之和能等于 2 005 吗?若能,请写出这五个数;若不能, 说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y= ![]() 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )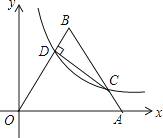
A.25 ![]()
B.18 ![]()
C.9 ![]()
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】OC把∠AOB分成两部分且有下列两个等式成立:
①∠AOC=![]() 直角+
直角+![]() ∠BOC;②∠BOC=
∠BOC;②∠BOC=![]() 平角-
平角-![]() ∠AOC,问∶
∠AOC,问∶
(1)OA与OB的位置关系怎样?
(2)OC是否为∠AOB的平分线?并写出判断的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com