
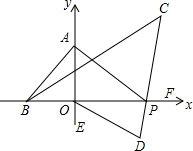
 如图,在平面直角坐标系中,∠ABO=2∠BAO,P为x轴正半轴一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE
如图,在平面直角坐标系中,∠ABO=2∠BAO,P为x轴正半轴一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE分析 (1)在RT△AOB中根据已知和两锐角互余的性质即可求出∠BAO的度数;
(2)根据外角的性质表示出∠C,得到∠C与∠OAP之间的数量关系;
(3)根据对顶角相等,分别表示出∠C和∠D,得到∠C+∠D的值.
解答 解:(1)∵∠AOB=90°,∠ABO=2∠BAO,
∴∠BAO=30°;
(2)∵∠APF=∠OAP+∠AOP,∠CBF=$\frac{1}{2}$∠ABO=30°
∴∠C=$\frac{1}{2}$∠APF-∠CBF
=$\frac{1}{2}$∠OAP+45°-30°=$\frac{1}{2}$∠OAP+15°
(3)∠C+∠D不变.
∠CPF=∠OPD,
∠CPF=∠C+30°,
∠OPD=180°-45°-∠D
∠C+30°=180°-45°-∠D
∠C+∠D=105°.
点评 本题考查的是三角形内角和定理、三角形的外角的性质、角平分线的定义,掌握定理、性质是解题的关键,解答时,注意结合图形正确写出各角之间的关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,点A从原点O出发,每次向上移动2个单位长度或向右移动1个单位长度.
在平面直角坐标系中,点A从原点O出发,每次向上移动2个单位长度或向右移动1个单位长度.| A从点O出发移动次数 | 可能到达的点的坐标 |
| 1次 | (0,2),(1,0) |
| 2次 | (0,4),(1,2),(2,0) |
| 3次 | (0,6),(1,4),(2,2),(3,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的点B′和点C′处,且∠C′DB′=60°,则点B′的坐标是(3,-$\sqrt{3}$).
如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的点B′和点C′处,且∠C′DB′=60°,则点B′的坐标是(3,-$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,在△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D,给出下列结论:①∠EAB=∠FAC;②AF=AC;③∠C=∠EFA;④AD=AC,其中正确的结论是①②③(填写所有正确结论的序号).
如图所示,在△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D,给出下列结论:①∠EAB=∠FAC;②AF=AC;③∠C=∠EFA;④AD=AC,其中正确的结论是①②③(填写所有正确结论的序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com