
【题目】如图,平行四边形ABCD中,AD=9cm,CD=![]() cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)
cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)

(1)求BC边上高AE的长度;
(2)连接AN、CM,当t为何值时,四边形AMCN为菱形;
(3)作MP⊥BC于P,NQ⊥AD于Q,当t为何值时,四边形MPNQ为正方形.
【答案】(1)3cm;(2)当t为![]() 时,四边形AMCN为菱形;(3)当t为4.5或1.5秒时,四边形MPNQ为正方形
时,四边形AMCN为菱形;(3)当t为4.5或1.5秒时,四边形MPNQ为正方形
【解析】
(1)先由平行四边形的性质得出AB=CD=3![]() cm.再解直角△ABE,即可求出AE的长度;
cm.再解直角△ABE,即可求出AE的长度;
(2)先证明四边形AMCN为平行四边形,则当AN=AM时,四边形AMCN为菱形.根据AN=AM列出方程32+(6-t)2=t2,解方程即可;
(3)先证明四边形MPNQ为矩形,则当QM=QN时,四边形MPNQ为正方形.根据QM=QN列出方程|2t-6|=3,解方程即可.
(1)∵四边形ABCD是平行四边形,
∴AB=CD=3![]() cm.
cm.
在直角△ABE中,∵∠AEB=90°,∠B=45°,
∴AE=ABsin∠B=3![]() ×
×![]() =3(cm);
=3(cm);
(2)∵点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6),
∴AM=CN=t,
∵AM∥CN,
∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
∵BE=AE=3,EN=|6-t|,
∴AN2=32+(6-t)2,
∴32+(6-t)2=t2,
解得t=![]() .
.
所以当t为![]() 时,四边形AMCN为菱形;
时,四边形AMCN为菱形;
(3)∵MP⊥BC于P,NQ⊥AD于Q,QM∥NP,
∴四边形MPNQ为矩形,
∴当QM=QN时,四边形MPNQ为正方形.
∵AM=CN=t,BE=3,
∴AQ=EN=BC-BE-CN=9-3-t=6-t,
∴QM=AM-AQ=|t-(6-t)|=|2t-6|(注:分点Q在点M的左右两种情况),
∵QN=AE=3,
∴|2t-6|=3,
解得t=4.5或t=1.5.
所以当t为4.5或1.5秒时,四边形MPNQ为正方形.



科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A坐标为(4,4),点B的坐标为(2,0).
(1)求线段AB的长;
(2)点M是坐标轴上的一个点,若以AB为直角边构造直角三角形△ABM,请求出满足条件的所有点M的坐标;
(3)如图2,以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴与点C,射线AD交y轴的负半轴与点D,当∠CAD绕点A旋转时,OCOD的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要求写解题过程).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市有5 000万人口,若平均每3.3人为一个家庭,平均每个家庭每周丢弃5个塑料袋,一年将丢弃多少个塑料袋?若每1 000个塑料袋污染1平方米土地,那么该城市一年被塑料袋污染的土地是多少?(保留2个有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
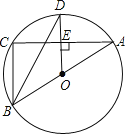
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校的学生人数基本相同,为了解这两所学校学生的数学学业水平,在同一次测试中,从两校各随机抽取了30名学生的测试成绩进行调査分析,其中甲校已经绘制好了条形统计图,乙校只完成了一部分.
甲校 | 54 | 68 | 69 | 76 | 76 | 76 | 76 | 77 | 79 | 82 | 83 | 83 | 84 | 84 | 87 |
87 | 87 | 88 | 88 | 89 | 89 | 89 | 89 | 89 | 90 | 92 | 92 | 92 | 93 | 94 | |
乙校 | 57 | 61 | 63 | 71 | 72 | 73 | 76 | 79 | 80 | 83 | 84 | 84 | 84 | 85 | 85 |
87 | 87 | 88 | 89 | 89 | 90 | 90 | 91 | 92 | 92 | 92 | 92 | 92 | 94 | 94 |
(1)请根据乙校的数据补全条形统计图;

(2)两组样本数据的平均数、中位数、众数如下表所示,请补全表格;
平均数 | 中位数 | 众数 | |
甲校 | 83.4 | 87 | 89 |
乙校 | 83.2 |
(3)两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些,请为他们各写出一条可以使用的理由;甲校: ;乙校; .
(4)综合来看,可以推断出 校学生的数学学业水平更好一些,理由为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在疫情期间的复学准备工作中,为了贯彻落实“生命重于泰山,安全至关重要”的思想,计划购买室内、室外两种型号的消毒液.已知每桶室外消毒液的价格比每桶室内消毒液的价格多30元,买2桶室内消毒液和3桶室外消毒液共需340元.
(1)求室内、室外两种型号消毒液每桶的价格;
(2)根据学校实际情况,需购买室内、室外两种型号的消毒液共200桶,总费用不高于1.4万元,问室内消毒液至少要购买多少桶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
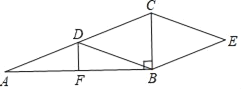
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com