Question

　　(常德市2003年中考试题)二次函数y=ax²+Bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③B²-4ac＞0；④＜0中，正确的结论有    (　)

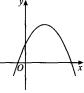
　　A．1个　　　　　　　　　　　　 B．2个

　　C．3个　　　　　　　　　　　　 D．4个

 

Answer 1

答案：D
解析：

解析：根据抛物线y=ax2+Bx+c的图象与a、B、c的关系，可以判定出结果． 　　∵　抛物线的开口向下，∴　a＜0．又∵　对称轴在y轴的右侧，∴　a、B异号．∴　＜0．又∵　抛物线与y轴的交点在y轴的正半轴上，∴　c＞0．由抛物线与x轴有两个交点，得B2-4ac＞0.∴　①②③④都正确． 　　点评：本题体现了数形结合法的应用，这是解决函数问题极为重要的数学方法．能借助函数的图象来研究函数的性质． 　　对于抛物线y=ax2+Bx+c有以下特点： 　　(1)a的符号由开口方向确定：开口向上，a＞0；开口向下，a＜0．简记作“上正下负”． 　　(2)B的符号由对称轴的位置和a的符号共同确定：对称轴在y轴的左侧，a、B同号；对称轴在y轴的右侧，a、B异号；对称轴在y轴上，B=0．简记作“左同右异，在y轴B=0”． 　　(3)c的符号由抛物线与y轴交点的位置确定：抛物线与y轴的交点在y轴的正半轴，c＞0；抛物线与y轴的交点在y轴的负半轴，c＜0；抛物线与y轴的交点在原点，c=0．简记作“上正下负，过原点c=0”． 　　(4)B2-4ac的符号由抛物线x轴交点的个数确定：抛物线与x轴有2个交点，B2-4ac＞0；抛物线与x轴有1个交点，B2-4ac=0；抛物线与x轴没有交点，则B2-4ac＜0．简记作“二正一零没有负”． 　　(5)a+B+c的符号由抛物线上横坐标为1的点的位置确定：抛物线上横坐标为1的点在x轴上方，a+B+c＞0；抛物线上横坐标为1的点在x轴的下方，a+B+c＜0；抛物线上横坐标为1的点在x轴上，a+B+c=0．简记作“上正下负，在x轴上等于0”． 　　(6)a-B+c的符号由抛物线上横坐标为-1的点的位置确定：抛物线上横坐标为-1的点在x轴的上方，a-B+c＞0；抛物线上横坐标为-1的点在x轴的下方，a-B+c＜0；抛物线上横坐标为-1的点在x轴上，a-B+c=0．简记作“上正下负，在x轴上等于0”．