
【题目】某修理厂需要购进甲、乙两种配件,经调查,每个甲种配件的价格比每个乙种配件的价格少0.4万元,且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同.
(1)求每个甲种配件、每个乙种配件的价格分别为多少万元;
(2)现投入资金80万元,根据维修需要预测,甲种配件要比乙种配件至少要多22件,问乙种配件最多可购买多少件.
【答案】(1) 每个甲种配件的价格为0.8万元、每个乙种配件的价格为1.2万元;(2) 乙种配件最多可购买31件.
【解析】(1)设每个乙种配件的价格为x万元,则每个甲种配件的价格为(x-0.4)万元,根据用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同列方程求解即可,分式方程要检验;
(2)设甲种配件为m件,乙种配件为n件,根据投入资金80万元,列方程求出m和n的关系,再根据甲种配件要比乙种配件至少要多22件得m-n≥22,从而求出n的最大值;
(1)设每个乙种配件的价格为x万元,则每个甲种配件的价格为(x-0.4)万元,
由题意得:![]() ,
,
解得,x=1.2,
经检验x=1.2是方程的解,
∴每个甲种配件的价格为0.8万元、每个乙种配件的价格为1.2万元;
(2)设甲种配件为m件,乙种配件为n件,
则:0.8m+1.2n=80,
∴ m=100-![]() n
n
∵甲种配件要比乙种配件至少要多22件,
∴m-n≥22,
∴100-![]() n-n≥22,∴n≤
n-n≥22,∴n≤![]() ,
,
∴乙种配件最多可购买31件,


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,等腰直角三角形ACB与ECD的顶点都在网格点上,点N、M分别为线段AB、DE上的动点,且BN=EM. (Ⅰ)如图①,当BN= ![]() 时,计算CN+CM的值等于
时,计算CN+CM的值等于 ![]()
(Ⅱ)当CN+CM取得最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段CN和CM,并简要说明点M和点N的位置是如何找到的(不要求证明).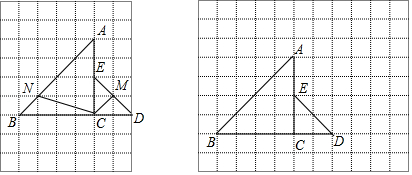
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠B、∠C的平分线交于P,且分别与AD交于E、F,
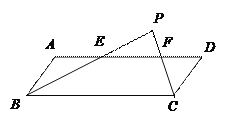
(1)求证:△BPC为直角三角形;
(2)若BC=16,CD=3,PE=8,求△PEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八达岭森林体验中心,由八达岭森林体验馆和450公顷的户外体验区构成。森林体验馆包括"八达岭森林变迁"、"八达岭森林大家族"、"森林让生活更美好"等展厅,户外游憩体验系统根据森林生态旅游最新理念,采取少设施、设施集中的点线布局模式,突破传统的"看风景"旅游模式,强调全面体验森林之美。
在室内展厅内,有这样一个可以动手操作体验的仪器,如图小明在社会大课堂活动中,记录了这样一组数字:

交通 工具 | 行驶100公里的碳足迹(Kg) | 100公里碳中 和树木棵树 |
飞机 | 13.9 | 0.06 |
小轿车 | 22.5 | 0.10 |
公共汽车 | 1.3 | 0.005 |
根据以上材料回答问题:
A,B两地相距300公里,小轿车以90公里/小时的速度从A地开往B地;公共汽车以60公里/小时的速度从B开往A地,两车同时出发相对而行,两车在C地相遇,相遇后继续前行到达各自的目的地。
(1)多少小时后两车相遇?
(2)小轿车和公共汽车分别到达目的地,计算小轿车的碳足迹为多少?公共汽车的碳中和树木棵数为多少?
(3)根据观察或计算说明,为了减少环境污染,我们应该选择哪种交通工具出行更有利于环保呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
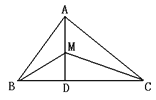
A. 9 B. 35 C. 45 D. 无法计算
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y= ![]() 的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )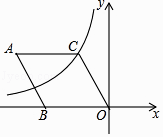
A.y=﹣ ![]()
B.y=﹣ ![]()
C.y=﹣ ![]()
D.y= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
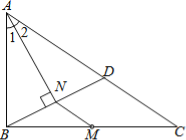
(1)求证:BN=DN;
(2)求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A. 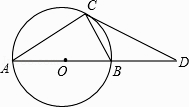
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com