
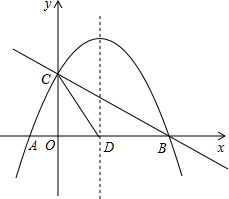
 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).分析 (1)利用待定系数法求二次函数的解析式;
(2)分四种情况讨论:
①如图1,PC=CD,根据等腰三角形三线合一的性质得:PD=2DG=2OC=4,再由抛物线的解析式求出对称轴,可以得出此时P点的坐标;
②如图2,CD=PD,利用勾股定理求出CD的长,即是PD的长,可以得出此时P点的坐标有两个;
③如图3,作CD的垂直平分线PN,可得等腰△PCD,设CN=DN=x,则DN=x-$\frac{3}{2}$,根据勾股定理分别求ND和PD的长,从而得出点P的坐标;
(3)如图4,作辅助线,将所求的△BEC分成了两个三角形,则面积等于这两个三角形的面积和,先求BC的解析式,表示出E、F两点的坐标,并求出EF的长,代入面积公式可求得△BEC,并求其最大值.
解答 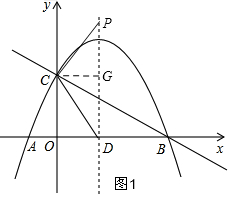 解:(1)把A(-1,0),C(0,2)代入y=-$\frac{1}{2}$x2+mx+n得:
解:(1)把A(-1,0),C(0,2)代入y=-$\frac{1}{2}$x2+mx+n得:
$\left\{\begin{array}{l}{-\frac{1}{2}-m+n=0}\\{n=2}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=\frac{3}{2}}\\{n=2}\end{array}\right.$
∴抛物线的解析式为:y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2;
(2)当△PCD为等腰三角形时,分四种情况讨论:
①如图1,当PC=CD时,△PCD为等腰三角形,
过C作CG⊥PD于G,则DG=PG,
y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-$\frac{1}{2}$(x-$\frac{3}{2}$)2+$\frac{25}{8}$,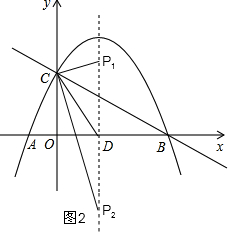
∴对称轴为:直线x=$\frac{3}{2}$,
当x=0时,y=2,
∴C(0,2),
∴OC=2,
∴DG=2,PD=4,
∴P($\frac{3}{2}$,4);
②如图2,当CD=PD时,△PCD为等腰三角形,
则OD=$\frac{3}{2}$,OC=2,
由勾股定理得:CD=$\sqrt{O{C}^{2}+O{D}^{2}}$=$\sqrt{{2}^{2}+(\frac{3}{2})^{2}}$=$\frac{5}{2}$,
∴P1D=P2D=CD=$\frac{5}{2}$,
∴P1($\frac{3}{2}$,$\frac{5}{2}$),P2($\frac{3}{2}$,-$\frac{5}{2}$);
③如图3,作CD的垂直平分线PN,交对称轴于P,交x轴于N,连接CN,
则DM=$\frac{1}{2}$CD=$\frac{5}{4}$,此时PC=PD,
设CN=DN=x,则DN=x-$\frac{3}{2}$,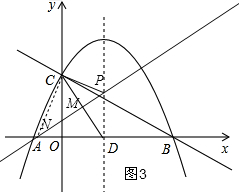
在Rt△ONC中,${x}^{2}={2}^{2}+(x-\frac{3}{2})^{2}$,
解得:x=$\frac{25}{12}$,
在Rt△NMD中,MN=$\sqrt{(\frac{25}{12})^{2}-(\frac{5}{4})^{2}}$=$\frac{5}{3}$,
tan∠PND=$\frac{DM}{MN}=\frac{PD}{ND}$,
∴$\frac{\frac{5}{4}}{\frac{5}{3}}$=$\frac{PD}{\frac{25}{12}}$,
∴PD=$\frac{25}{16}$,
∴P($\frac{3}{2}$,$\frac{25}{16}$);
综上所述,点P的坐标有四个,分别是($\frac{3}{2}$,4)或($\frac{3}{2}$,$\frac{5}{2}$)或($\frac{3}{2}$,-$\frac{5}{2}$)或($\frac{3}{2}$,$\frac{25}{16}$);
(3)当y=0时,-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0,
解得:x1=-1,x2=4,
∴B(4,0),
设直线BC的解析式为:y=kx+b,
把B(4,0)、C(0,2)代入得:$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴直线BC的解析式为:y=-$\frac{1}{2}$x+2,
如图4,过E作EF∥y轴,交直线BC于点F,交x轴于N,过C作CM⊥EF于M,
设E(x,-$\frac{1}{2}$x2+$\frac{3}{2}$x+2),则F(x,-$\frac{1}{2}$x+2),
∴EF=(-$\frac{1}{2}$x2+$\frac{3}{2}$x+2)-(-$\frac{1}{2}$x+2)=-$\frac{1}{2}{x}^{2}$+2x(0<x<4),
∵S△ABE=S△CEF+S△BEF=$\frac{1}{2}$EF•CM+$\frac{1}{2}$EF•BN,
=$\frac{1}{2}$EF(CM+BN)
=$\frac{1}{2}$EF•OB
=$\frac{1}{2}$×4(-$\frac{1}{2}{x}^{2}$+2x),
=-x2+4x,
=-(x-2)2+4(0<x<4),
∴当x=2时,△ABE的面积最大为4,此时E(2,2).
点评 本题是二次函数的综合题,考查了利用待定系数法求二次函数和一次函数的解析式、二次函数的性质、勾股定理及同角的三角函数;难度适中,在考虑构建等腰三角形时,采用了分类讨论的思想,并借助线段垂直平分线的性质;将三角形面积的最大值问题转化为二次函数的最值问题来解决.


科目:初中数学 来源: 题型:填空题
 某校为了美化校园,准备在一块长a米,宽b米的长方形场地上修筑横纵各一条道路,道路宽度均为x米,(如图所示)余下部分作草坪,则草坪面积用代数式表示为(a-x)(b-x).
某校为了美化校园,准备在一块长a米,宽b米的长方形场地上修筑横纵各一条道路,道路宽度均为x米,(如图所示)余下部分作草坪,则草坪面积用代数式表示为(a-x)(b-x).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
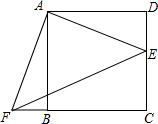 如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
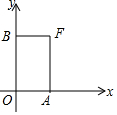 在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAFB的周长与面积相等,则点F是和谐点.
在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAFB的周长与面积相等,则点F是和谐点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
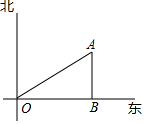 如图,小颖家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的400米处,那么水塔所在的位置到公路的距离AB是( )
如图,小颖家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的400米处,那么水塔所在的位置到公路的距离AB是( )| A. | 200米 | B. | 200$\sqrt{3}$米 | C. | $\frac{400}{3}$$\sqrt{3}$米 | D. | 400$\sqrt{2}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象必经过点(-1,2) | B. | y随x的增大而增大 | ||
| C. | 图象在第二、四象限内 | D. | 若y=1,则x=-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com