
【题目】如图,等腰三角形![]() 中,
中,![]() ,
,![]() 分别是两腰上的中线.
分别是两腰上的中线.
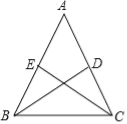
(1)求证:![]() ;
;
(2)设![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() ,
,![]() 分别为线段
分别为线段![]() 和
和![]() 的中点.当
的中点.当![]() 的重心到顶点
的重心到顶点![]() 的距离与底边长相等时,判断四边形
的距离与底边长相等时,判断四边形![]() 的形状,无需说明理由.
的形状,无需说明理由.
【答案】(1)证明见解析;(2)四边形DEMN是正方形.
【解析】
试题分析:(1)根据已知条件得到AD=AE,根据全等三角形的性质即可得到结论;
(2)根据三角形中位线的性质得到ED∥BC,ED=![]() BC,MN∥BC,MN=
BC,MN∥BC,MN=![]() BC,等量代换得到ED∥MN,ED=MN,推出四边形EDNM是平行四边形,由(1)知BD=CE,求得DM=EN,得到四边形EDNM是矩形,根据全等三角形的性质得到OB=OC,由三角形的重心的性质得到O到BC的距离=
BC,等量代换得到ED∥MN,ED=MN,推出四边形EDNM是平行四边形,由(1)知BD=CE,求得DM=EN,得到四边形EDNM是矩形,根据全等三角形的性质得到OB=OC,由三角形的重心的性质得到O到BC的距离=![]() BC,根据直角三角形的判定得到BD⊥CE,于是得到结论.
BC,根据直角三角形的判定得到BD⊥CE,于是得到结论.
试题解析:(1)由题意得,AB=AC,
∵BD,CE分别是两腰上的中线,∴AD=![]() AC,AE=
AC,AE=![]() AB,∴AD=AE,
AB,∴AD=AE,
在△ABD和△ACE中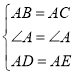 ,∴△ABD≌△ACE(ASA).∴BD=CE;
,∴△ABD≌△ACE(ASA).∴BD=CE;
(2)四边形DEMN是正方形,
理由:∵E、D分别是AB、AC的中点,∴AE=![]() AB,AD=
AB,AD=![]() AC,ED是△ABC的中位线,∴ED∥BC,ED=
AC,ED是△ABC的中位线,∴ED∥BC,ED=![]() BC,
BC,
∵点M、N分别为线段BO和CO中点,∴OM=BM,ON=CN,MN是△OBC的中位线,∴MN∥BC,MN=![]() BC,∴ED∥MN,ED=MN,∴四边形EDNM是平行四边形,由(1)知BD=CE,
BC,∴ED∥MN,ED=MN,∴四边形EDNM是平行四边形,由(1)知BD=CE,
又∵OE=ON,OD=OM,OM=BM,ON=CN,∴DM=EN,∴四边形EDNM是矩形,
在△BDC与△CEB中,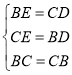 ,∴△BDC≌△CEB,∴∠BCE=∠CBD,∴OB=OC,
,∴△BDC≌△CEB,∴∠BCE=∠CBD,∴OB=OC,
∵△ABC的重心到顶点A的距离与底边长相等,∴O到BC的距离=![]() BC,∴BD⊥CE,
BC,∴BD⊥CE,
∴四边形DEMN是正方形.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.

(1)求二次函数的解析式和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,当点
,当点![]() 在第一象限时,求线段
在第一象限时,求线段![]() 长度的最大值;
长度的最大值;
(3)在抛物线上是否存在异于![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高为
边上的高为![]() ,若存在求出点
,若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知一次函数y=﹣2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1_____y2.(填“>”“<”“=”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com