
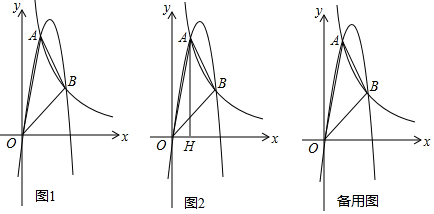
���� ��1�����ô���ϵ�������k��a��m���ɣ�
��2����ȷ����ֱ��AB����ʽ�����������ε����֮��ɵ�������AOB�������
��3���ֵ�D��ֱ��OB�Ϸ��������ߺ��·����������ϣ�����ͬ��ͬ��ȸ߽������̼������ֱ��AD�Ľ���ʽ�����������鼴�ɵó���D�����ꣻ
��4�����˶��ص㿴����M�͵�A�غ�ʱ����������t��С����MԽ���£�t��ֵԽ��BM��ֱ��AHʱ����N�պú͵�H�غϣ���ʱ��ʱ��Ϊ1�����ɵó�����������t�ķ�Χ��
��� �⣺��1����˫����y=$\frac{k}{x}$��������y=a��x-$\frac{4}{3}$��2+m��һ������A��B���㣬��֪A��1��4����B��2��2����
��k=1��4=4��
$\left\{\begin{array}{l}{a��1-\frac{4}{3}��^{2}+m=4}\\{a��2-\frac{4}{3}��^{2}+m=2}\end{array}\right.$��
��$\left\{\begin{array}{l}{a=-6}\\{m=\frac{14}{3}}\end{array}\right.$��
����k=4��a=-6��m=$\frac{14}{3}$��
��2����A��1��4����B��2��2����
��ֱ��AB����ʽΪy=-2x+6��
��ֱ��AB��y��Ľ���ΪE��
��E��0��6����
��OE=6��
��S��AOB=$\frac{1}{2}$OE����xB-xA��=$\frac{1}{2}$��6����2-1��=3��
��3���ɣ�1���ó��������ߵĽ���ʽΪy=-6��x-$\frac{4}{3}$��2+$\frac{14}{3}$=-6x2+16x-6�٣�
�ٵ�D��ֱ��OB�Ϸ�����������ʱ��
��B��2��2����
��ֱ��OB����ʽΪy=x��
����A��AD��OB��
��A��1��4����
��AD�Ľ���ʽΪy=x+3�ڣ�
�����٢ڵã�D��$\frac{3}{2}$��$\frac{9}{2}$����
����ͼ1��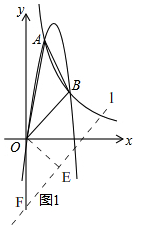
����D��ֱ��OB�·�����������ʱ��
��B��2��2����
��OB=2$\sqrt{2}$��
�ɣ�2��֪��S��AOB=3��
���AOB��OB���ϵĸ�Ϊh=6��OB=6��2$\sqrt{2}$=$\frac{3\sqrt{2}}{2}$��
��ֱ��l��OB����y����F������O��OE��l��E��
��OE=$\frac{3\sqrt{2}}{2}$��
�ߡ�BOx=45�㣬
���EOx=45�㣬
���EOF=45�㣬
��OF=$\sqrt{2}$OE=3��
��F��0��-3����
��ֱ��l�Ľ���ʽΪy=x-3�ۣ�
�����٢۵õ�D��$\frac{5+\sqrt{17}}{4}$��$\frac{\sqrt{17}-7}{4}$����$\frac{5-\sqrt{17}}{4}$��$\frac{-\sqrt{17}-7}{4}$����
��������������D������ΪD��$\frac{3}{2}$��$\frac{9}{2}$����$\frac{5+\sqrt{17}}{4}$��$\frac{\sqrt{17}-7}{4}$����$\frac{5-\sqrt{17}}{4}$��$\frac{-\sqrt{17}-7}{4}$����
��4������BMN=90��ʱ
����M�͵�A�غ�ʱ��t����С�ģ�
����A��ֱ��AN��AB��
�ɣ�2��֪��ֱ��AB����ʽΪy=-2x+6��
��A��1��4����
��ֱ��AN�Ľ���ʽΪy=$\frac{1}{2}$x+$\frac{9}{2}$��
��y=0�����x=-9��
��t��СΪ-9��
����N�͵�H�غ�ʱ����ʱt=1��
��M���߶�AH�ϵ�һ���㣬N��t��0����x������H����һ���㣬
��-9��t��1��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ�����������ε������ʽ��ͬ��ͬ��ȸߵ��������������ȣ�ֱ�ǵ����ʣ��Ȿ��Ĺؼ�����ͬ��ͬ��ȸߵ�����������������������⣬Ҳ�ǽⱾ����ѵ㣬��һ���п������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ƽ���ҵ�ֱ����ֱ���� | |
| B�� | ��ȵ�Բ�Ľ����ԵĻ���� | |
| C�� | ��Բ����ֱ�������Ե�Բ�ܽ���ֱ�� | |
| D�� | ��ֱ�ߺ�Բ�й����㣬��ֱ�ߺ�Բ�ཻ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 2 | C�� | 6 | D�� | 54 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com