
【题目】本学期我们学习了“有理数乘方”运算,知道乘方的结果叫做“幂”,下面介绍一种有关“幂”的新运算.
定义:am 与 an(a≠0,m、n 都是正整数)叫做同底数幂,同底数幂除法记作 am÷an .
运算法则如下:am÷an=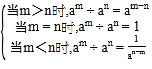
根据“同底数幂除法”的运算法则,回答下列问题:
(1)填空:![]() = ,43÷45= .
= ,43÷45= .
(2)如果 3x-1÷33x-4=![]() ,求出 x 的值.
,求出 x 的值.
(3)如果(x﹣1)2x+2÷(x﹣1)x+6=1,请直接写出 x 的值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( ) 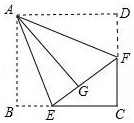
A.1.5
B.2.5
C.2.25
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.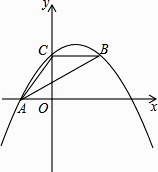
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题的提出:如果点P是锐角![]() 内一动点,如何确定一个位置,使点P到
内一动点,如何确定一个位置,使点P到![]() 的三顶点的距离之和
的三顶点的距离之和![]() 的值为最小?
的值为最小?
![]() 问题的转化:把
问题的转化:把![]() 绕点A逆时针旋转
绕点A逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,这样就把确定
,这样就把确定![]() 的最小值的问题转化成确定
的最小值的问题转化成确定![]() 的最小值的问题了,请你利用图1证明:
的最小值的问题了,请你利用图1证明:![]() ;
;
![]() 问题的解决:当点P到锐角
问题的解决:当点P到锐角![]() 的三顶点的距离之和
的三顶点的距离之和![]() 的值为最小时,求
的值为最小时,求![]() 和
和![]() 的度数;
的度数;
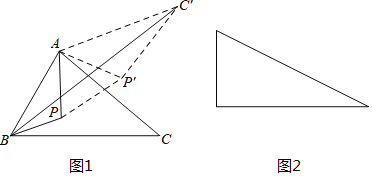
![]() 问题的延伸:如图2是有一个锐角为
问题的延伸:如图2是有一个锐角为![]() 的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+ ![]() )海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段MN=3cm,在线段MN上取一点P,使PM=PN;延长线段MN到点A,使AN=![]() MN;延长线段NM到点B,使BN=3BM.
MN;延长线段NM到点B,使BN=3BM.
(1)根据题意,画出图形;
(2)求线段AB的长;
(3)试说明点P是哪些线段的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= ![]() .
.
其中正确的结论有( )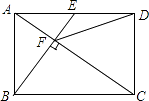
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.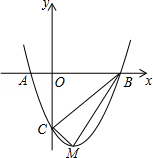
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com