
请在图中补全坐标系及缺失的部分,并在横线上写恰当的内容。图中各点坐标如下:A(1,0),B(6,0),C(1,3),D(6,2)。线段AB上有一点M,使△ACM∽△BDM,且相似比不等于1。求出点M的坐标并证明你的结论。
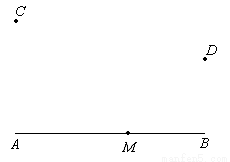
解:M( , )
证明:∵CA⊥AB,DB⊥AB,∴∠CAM=∠DBM= 度。
∵CA=AM=3,DB=BM=2,∴∠ACM=∠AMC( ),∠BDM=∠BMD(同理),
∴∠ACM=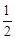 (180°- ) =45°。 ∠BDM=45°(同理)。
(180°- ) =45°。 ∠BDM=45°(同理)。
∴∠ACM=∠BDM。
∴△ACM∽△BDM(如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似)。
科目:初中数学 来源: 题型:
 (2013•河池)请在图中补全坐标系及缺失的部分,并在横线上写恰当的内容.图中各点坐标如下:A(1,0),B(6,0),C(1,3),D(6,2).线段AB上有一点M,使△ACM∽△BDM,且相似比不等于1.求出点M的坐标并证明你的结论.
(2013•河池)请在图中补全坐标系及缺失的部分,并在横线上写恰当的内容.图中各点坐标如下:A(1,0),B(6,0),C(1,3),D(6,2).线段AB上有一点M,使△ACM∽△BDM,且相似比不等于1.求出点M的坐标并证明你的结论.| 1 |
| 2 |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com