练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
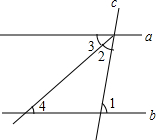
    1．如图，直线a，b被直线c所截，a∥b，∠2=∠3，若∠1=80°，则∠4等于（　　）
    A．20°B．40°C．60°D．80°

    分析 先根据平行线的性质求出∠2+∠3的度数，再由∠2=∠3即可得出结论．

    解答 解：∵a∥b，∠1=80°，
    ∴∠2+∠3=80°，∠3=∠4．
    ∵∠2=∠3，
    ∴∠3=40°，
    ∴∠4=40°．
    故选B．

    点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．如图1，E是直线AB，CD内部一点，AB∥CD，连接EA，ED．
    （1）探究猜想：①∠A=30°，∠D=40°，则∠AED等于多少度？
    ②若∠A=20°，∠D=60°，则∠AED等于多少度？
    ③猜想图1中∠AED、∠EAB、∠EDC的关系并说明理由．
    （2）拓展应用，如图2，线段FE与长方形ABCD的边AB交于点E，与边CD 交于点F．图2中①②分别是被线段FE隔开的2个区域（不含边界），P是位于以上两个区域内的一点，猜想∠PEB，∠PFC，∠EPF的关系（不要求说明理由）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．写出方程5x-3y=4的一个解，要求满足：
    （1）x、y相等：$\left\{\begin{array}{l}{x=___}\\{y=___}\end{array}\right.$，（2）x、y互为相反数：$\left\{\begin{array}{l}{x=___}\\{y=___}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．某校初三学生开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀．下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）：
    1号2号3号4号5号总数
    甲班1009811089103500
    乙班891009511997500
    经统计发现两班总数相等．此时有学生建议，可以通过考察数据中的其他信息作为参考．
    请你回答下列问题：
    （1）填空：甲班的优秀率为60%，乙班的优秀率为40%；
    （2）填空：甲班比赛数据的中位数为100，乙班比赛数据的中位数为97；
    （3）填空：估计两班比赛数据的方差较小的是甲班（填甲或乙）
    （4）根据以上三条信息，你认为应该把冠军奖状发给哪一个班级？简述你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．某学校为了解在校生的体能素质情况，从全校八年级学生中随机抽取了部分学生进行了一次体育科目测试（把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格）并将测试结果绘成了如下两幅不完整的统计图，请根据统计图中的信息解答下列问题：
    （1）本次抽样测试的学生人数是40；
    （2）扇形统计图中∠α的度数是54°，并把条形统计图补充完整；
    （3）该校八年级有学生1500名，如果全部参加这次体育科目测试，那么估计不及格的人数为0.3；
    （4）测试老师从被测学生中随机抽取一名，所抽学生为B级的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

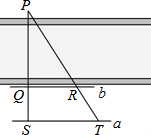    6．如图，为了估计河的宽度，在河的对岸选定一个目标点P，在近岸取点Q和S，使点P，Q，S在一条直线上，且直线PS与河垂直，在过点S且与PS垂直的直线a上选择适当的点T，PT与过点Q且与PS垂直的直线b的交点为R．如果QS=60m，ST=120m，QR=80m，则河的宽度PQ为（　　）
    A．40mB．60mC．120mD．180m

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知关于x的一元二次方程x2-6x+k+3=0有两个不相等的实数根?
    （1）求k的取值范围；
    （2）若k为大于3的整数，且该方程的根都是整数，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．根据某市统计局提供的2010～2014年该市地铁运营的相关数据，绘制的统计图表如下：

    根据以上信息解答下列问题：
    （1）直接写出“2014年某市居民乘地铁出行距离情况统计图”中m的值；
    （2）从2010年到2014年，该市地铁的日均客流量每年的增长率近似相等，估算2015年该市地铁运营的日均客流量约为483万人次；
    （3）自2015年起，该市地铁运营实行了新票价：乘地铁5公里内（含5公里）收费2元，乘地铁5～15公里（含15公里）收费3元，乘地铁15公里以上收费4元．如果2015年该市居民乘地铁出行距离情况与2014年基本持平，估算2015年该市地铁运营平均每日票款收入约为1593.9万元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，在等腰Rt△OAA1中，∠OAA1=90°，OA=1，以OA1为直角边作等腰Rt△OA1A2，以OA2为直角边作等腰Rt△OA2A3，…，则OAn的长度为$\sqrt{{2}^{n}}$．

    查看答案和解析>>

    同步练习册答案