
 如图,以△ABC的各边为边分别向外作正方形,所得到的三个正方形的面积分别为S1=36,S2=64,S3=100,则△ABC的面积是( )
如图,以△ABC的各边为边分别向外作正方形,所得到的三个正方形的面积分别为S1=36,S2=64,S3=100,则△ABC的面积是( ) 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:初中数学 来源: 题型:
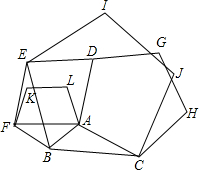 (2012•拱墅区一模)如图,以△ABC的各边为边,在BC的同侧分别作三个正五边形.它们分别是正五边形ABFKL、BCJIE、ACHGD,试探究:
(2012•拱墅区一模)如图,以△ABC的各边为边,在BC的同侧分别作三个正五边形.它们分别是正五边形ABFKL、BCJIE、ACHGD,试探究:查看答案和解析>>
科目:初中数学 来源: 题型:
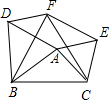 如图,以△ABC的各边向同侧作正△ABD,BCF,ACE.
如图,以△ABC的各边向同侧作正△ABD,BCF,ACE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com