
【题目】(2017浙江省湖州市)如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是______.

科目:初中数学 来源: 题型:
【题目】年是我市“创建国家卫生城市”第一年,为了了解本班![]() 名学生对“创卫”的知晓率,某同学采取随机抽样的方法进行问卷调查,调查分为四个选项:
名学生对“创卫”的知晓率,某同学采取随机抽样的方法进行问卷调查,调查分为四个选项:![]() 非常了解,
非常了解,![]() 比较了解,
比较了解,![]() 基本了解,
基本了解,![]() 不甚了解.数据整理如下:
不甚了解.数据整理如下:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
请画出条形图和扇形图来描述以上统计数据.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”期间,某风景区在7天中每天游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 单位:万人 |
|
|
|
|
|
|
|
(1)若9月30日的游客人数记为![]() ,请用含
,请用含![]() 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)此风景区一方面给广大市民提供一个休闲游玩的好去处;另一方面拉动了内需,促进了消费.若9月30日的游客人数为1万人,进园的人每人平均消费60元,问“十一”期间所有游园人员在此风景区的总消费是多少元?(用科学记数法表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣3x+k=0方程有两实根x1和x2.
(1)求实数k的取值范围;
(2)当x1和x2是一个矩形两邻边的长且矩形的对角线长为![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点A(1,0)和B(0,3),其顶点为D.
经过点A(1,0)和B(0,3),其顶点为D.
(1)求此抛物线的表达式;
(2)求△ABD的面积;
(3)设P为该抛物线上一点,且位于抛物线对称轴右侧,作PH⊥对称轴,垂足为H,若△DPH与△AOB相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分隔成ABABC共5个区,A区是边长为a m的正方形,C区是4个边长为b m的小正方形组成的正方形.

(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40 m,b=20 m,求整个长方形运动场的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在透明纸面上有一数轴(如图1),折叠透明纸面.
(1)若表示![]() 的点与表示
的点与表示![]() 的点重合,则表示
的点重合,则表示![]() 的点与表示_________的点重合;
的点与表示_________的点重合;
(2)若表示![]() 的点与表示
的点与表示![]() 的点重合,回答以下问题:
的点重合,回答以下问题:
①表示![]() 的点与表示__的点重合;
的点与表示__的点重合;
②如图2,若数轴上![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() (点
(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() 、
、![]() 两点经折叠后重合,则
两点经折叠后重合,则![]() 、
、![]() 两点表示的数分别是_________、_________.
两点表示的数分别是_________、_________.
(3)如图3,若![]() 和
和![]() 表示的点
表示的点![]() 和点
和点![]() 经折叠后重合
经折叠后重合![]() ,折痕与数轴的交点为折痕点.已知线段
,折痕与数轴的交点为折痕点.已知线段![]() 上两点
上两点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧,
的左侧,![]() ),
),![]() .当线段
.当线段![]() 的端点与折痕点重合时,求
的端点与折痕点重合时,求![]() 、
、![]() 两点表示的数分别是多少?(用含
两点表示的数分别是多少?(用含![]() ,
,![]() ,
,![]() 的代数式表示).
的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=![]() (x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为_____.
(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
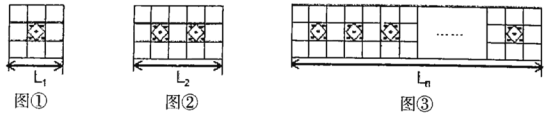
【题目】如图,学校准备新建一个长度为L的读书长廊,并准备用若干块带有花纹和没有花纹的两种规格大小相同的正方形地面砖搭配在一起,按图中所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.5m.
(1)按图示规律,第一图案的长度L1= m;第二个图案的长度L2= m.
(2)请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln(m)之间的关系;
(3)当走廊的长度L为20.5m时,请计算出所需带有花纹图案的瓷砖的块数,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com