
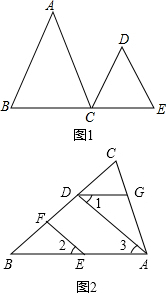
 (1)已知:如图,AB∥CD,∠A=∠D.试说明AC∥DE成立的理由.下面是某同学进行的推理.请你将他的推理过程补充完整.
(1)已知:如图,AB∥CD,∠A=∠D.试说明AC∥DE成立的理由.下面是某同学进行的推理.请你将他的推理过程补充完整.分析 (1)由平行线的性质和已知条件得出∠ACD=∠D,即可得出结论;
(2)由平行线的性质和已知条件得出∠1=∠3,证出AB∥DG,再由平行线的性质即可得出结果.
解答 (1)解:∵AB∥CD (已知)
∴∠A=∠ACD (两直线平行,内错角相等)
又∵∠A=∠D (已知)
∴∠ACD=∠D (等量代换)
∴AC∥DE (内错角相等,两直线平行)
故答案为:ACD,两直线平行,内错角相等;ACD,D,内错角相等,两直线平行;
(2)解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2 (已知)
∴∠l=∠3
∴AB∥DG(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补)
又∵∠BAC=70°(已知)
∴∠AGD=110°.
故答案为:∠3,两直线平行,同位角相等;DG,内错角相等,两直线平行;∠AGD,两直线平行,同旁内角互补;110°
点评 本题考查了平行线的判定与性质;熟练掌握平行线的判定与性质,注意它们之间的区别.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源:2017届江苏省江阴市周庄学区九年级下学期第一次模拟考试数学试卷(解析版) 题型:单选题
如图,⊙A经过点E、B、C、O,且C(0,8),E( 6,0),O(0,0),则cos∠OBC的值为( )
6,0),O(0,0),则cos∠OBC的值为( )
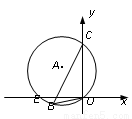
A.  B.
B.  C.
C.  D.
D. 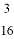
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
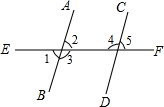 如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有( )
如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | 2 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com