
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)连接![]() ,在直线
,在直线![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() ,连接
,连接![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,当
,当![]() 时, 求
时, 求![]() 的值;
的值;
(3)点![]() 是直线
是直线![]() 上一点,在平面内是否存在点
上一点,在平面内是否存在点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
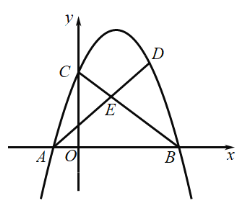
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)将![]() ,
,![]() 代入
代入![]() 得出关于a,b的二元一次方程,求解即可;
得出关于a,b的二元一次方程,求解即可;
(2)过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 与点
与点![]() ,交
,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 与点
与点![]() ,证明
,证明![]() ,得出
,得出![]() ,设
,设![]() ,
,![]() ,可得出关于t的方程,解出t值,即可得出答案;
,可得出关于t的方程,解出t值,即可得出答案;
(3)分①当PC为菱形的边时,②当PC为对角线时,两种情况讨论即可.
(1)将![]() ,
,![]() 代入
代入![]()
得![]() ,解得
,解得
![]() 解析式为
解析式为![]() ;
;
(2)当![]() 时
时![]()
![]()
设直线![]() 的解析式为
的解析式为![]() ,将
,将![]() ,
,![]() 分别代入得:
分别代入得:![]()
过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 与点
与点![]() ,交
,交![]() 轴于点
轴于点![]()
过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 与点
与点![]()
![]()
![]() 当
当![]() 时
时![]()
![]() ,
,![]()
![]() 轴
轴![]()
![]()
![]()

![]()
设![]() ,
,![]()
![]()
解得:![]()
![]()
![]() ,
,![]()
在![]() 中,
中, ;
;
(3)设直线BC的解析式为:y=kx+b,
将B(4,0),C(0,3)代入得![]() ,
,
解得 ,
,
∴直线BC的解析式为:y=![]() x+3,
x+3,
①当PC为菱形的边时,
∵四边形PQCA是菱形,
∴AQ∥PC,
可设AQ的解析式为:y=![]() x+b1,
x+b1,
将点A(-1,0)代入得b1=![]() ,
,
∴AQ的解析式为:y=![]() x
x![]() ,
,
∴可设Q(m,![]() m
m![]() ),
),
根据勾股定理得AC的长为![]() ,
,
根据菱形的性质可得AC=AQ,
∴![]() =
= ,
,
解得m=![]() ,
,
∴m1=![]() ,m2=
,m2=![]() ,
,
将m1,m2代入y=![]() x
x![]() ,
,
可得![]() ,
,![]() ;
;
②当PC为对角线时,
根据菱形的性质可得AQ⊥PC,
∴可设AQ的解析式为:y=![]() x+b3,
x+b3,
将A(-1,0)代入得b3=![]() ,
,
∴AQ的解析式为:y=![]() x+
x+![]() ,
,
∴可设Q(n,![]() n+
n+![]() ),
),
根据菱形的性质可得AC=CQ,
∴![]() =
= ,
,
解得n1=-5,n2=![]() ,
,
将n1,n2代入y=![]() x+
x+![]() ,
,
可得![]() ,
,![]() ;
;
综上,Q点的坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
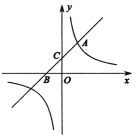
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() (
(![]() 为常数,
为常数,![]() )的图像在第一象限内交于点
)的图像在第一象限内交于点![]() ,且与
,且与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点.
两点.
(1)求一次函数和反比例函数的表达式;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() 的面积等于
的面积等于![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某剧院举行专场音乐会,成人票每张20元,学生票每张5元.暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案一:购买一张成人票赠送一张学生票;方案二:按总价的90%付款.某校有4名老师带队,与若干名(不少于4人)学生一起听音乐会.设学生人数为x人,![]() (x为整数).
(x为整数).
(Ⅰ)根据题意填表:
学生人数/人 | 4 | 10 | 20 | … |
方案一付款金额/元 | 80 | 110 | … | |
方案二付款金额/元 | 90 | 117 | … |
(Ⅱ)设方案一付款总金额为![]() 元,方案二付款总金额为
元,方案二付款总金额为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)根据题意填空:
①若用两种方案购买音乐会的花费相同,则听音乐会的学生有________________人;
②若有60名学生听音乐会,则用方案_______________购买音乐会票的花费少;
③若用一种方案购买音乐会票共花费了450元,则用方案________________购买音乐会票,使听音乐的学生人数多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
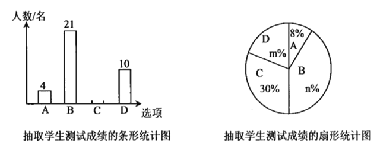
月![]() 日,葫芦岛市九年级师生结束了两个多月的线上教学和学习,正式回归校园,在开学第一天,某校教导处老师为了解九年级学生对“新冠”传播与防治知识的掌握情况,随机抽取了部分学生进行了防疫知识的测试,测试后的成绩,按得分划分为
日,葫芦岛市九年级师生结束了两个多月的线上教学和学习,正式回归校园,在开学第一天,某校教导处老师为了解九年级学生对“新冠”传播与防治知识的掌握情况,随机抽取了部分学生进行了防疫知识的测试,测试后的成绩,按得分划分为![]() 四个等级,
四个等级,![]() :优秀,
:优秀,![]() :良好,
:良好,![]() :及格,
:及格,![]() :不及格,并绘制了如下不完整的条形统计图和扇形统计图.根据提供的信息,解答以下问题:
:不及格,并绘制了如下不完整的条形统计图和扇形统计图.根据提供的信息,解答以下问题:
(1)本次调查抽取的学生人数有多少人?
(2)扇形统计图中![]() ,
,![]() 并补全条形统计图;
并补全条形统计图;
(3)已知该校九年级有![]() 名学生,学校决定对“不及格”的学生进行一次防疫知识的培训,那么需要接受培训的学生大约有多少人?
名学生,学校决定对“不及格”的学生进行一次防疫知识的培训,那么需要接受培训的学生大约有多少人?
(4)已知“优秀”的同学有![]() 名男生和
名男生和![]() 名女生,从中随机抽取
名女生,从中随机抽取![]() 名进行防疫知识的交流,请用画树状图或列表的方法,求恰好抽到一男一女的概率.
名进行防疫知识的交流,请用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E、F.

(1)求证:四边形AECF是菱形;
(2)当BE=3,AF=5时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘凯随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如图所示的统计图:
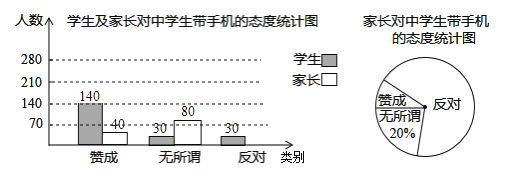
(1)求这次调查的家长人数,并补全图①:
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)从这次接受调查的学生中,随机抽查一个,恰好是“无所谓”态度的学生的概率是多少?
(4)为更深入的了解学生的看法,又从“赞成”的学生甲、乙、丙、丁四人中随机选取2人,请用树状图法或列表法求出恰好选中甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“食品安全”受到全社会的广泛关注,育才中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
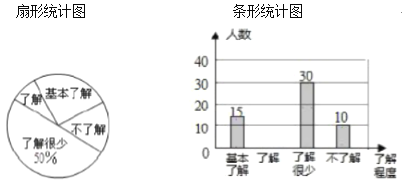
(1)接受问卷调查的学生共有________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_________![]() ;
;
(2)请补全条形统计图;
(3)若对食品安全知识达到“了解”程度的学生中,男、女生的比例恰为![]() ,现从中随机抽取
,现从中随机抽取![]() 人参加食品安全知识竞赛,则恰好抽到
人参加食品安全知识竞赛,则恰好抽到![]() 个男生和
个男生和![]() 个女生的概率________.
个女生的概率________.
查看答案和解析>>
科目:初中数学 来源: 题型:
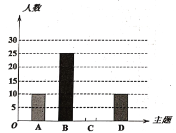
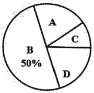
【题目】某校开展了“创建文明校园”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“A”所在扇形的圆心角等于 度;
(4)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式,求他们恰好同时选中“文明礼仪”或“生态环境”主题的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com