
【题目】解方程:
(1)x2﹣6x﹣6=0
(2)2x2﹣7x+6=0.
【答案】
(1)解:x2﹣6x﹣6=0,
b2﹣4ac=(﹣6)2﹣4×1×(﹣6)=60,
x= ![]() ,
,
x1=3+ ![]() ,x2=3﹣
,x2=3﹣ ![]() ;
;
(2)解:2x2﹣7x+6=0,
(2x﹣3)(x﹣2)=0,
2x﹣3=0,x﹣2=0,
x1= ![]() ,x2=2.
,x2=2.
【解析】(1)求出b2﹣4ac的值,代入公式求出即可;(2)先分解因式,即可得出两个一元一次方程,求出方程的解即可.
【考点精析】根据题目的已知条件,利用公式法的相关知识可以得到问题的答案,需要掌握要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之.


科目:初中数学 来源: 题型:
【题目】A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是 (填![]() 或
或![]() );
);
(2)甲的速度是 km/h,乙的速度是 km/h;
(3)甲出发多少小时两人恰好相距5km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的东南方向上的B处.这时,海轮所在的B处距离灯塔P有多远?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2﹣mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM,交x轴于点N,点D为OA的中点.
(1)求证:CD是⊙M的切线;
(2)求线段ON的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知等边△OAB的顶点A在反比例函数y= ![]() (x>0)图象上,当等边△OAB的顶点B在坐标轴上时,求等边△OAB顶点A的坐标和△OAB的面积.
(x>0)图象上,当等边△OAB的顶点B在坐标轴上时,求等边△OAB顶点A的坐标和△OAB的面积. 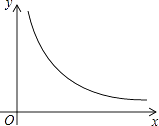
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,△ABC是等腰直角三角形,∠BAC=90°,DE是经过点A的直线,作BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com