
 ��ͼ����ƽ��ֱ������ϵ�У�˫����y=$\frac{1}{x}$��һ�κ���y=kx+b��k��0���ֱ��ڵ�A���B��ֱ����y�ύ�ڵ�C����ֱ��AB���ŵ�C��תһ���ĽǶȺõ�һ����ֱ�ߣ�����ֱ����˫����y=-$\frac{1}{x}$�ཻ�ڵ�E��F����ʹ��˫����y=$\frac{1}{x}$��y=-$\frac{1}{x}$������y=kx+b�Լ���ֱ�߹��ɵ�ͼ���ܹ���ij��������Գƣ������A�ĺ�����Ϊ1����kΪ����ʱ����A����E����B����F���ɵ��ı��ε������С����Сֵ�Ƕ��٣�
��ͼ����ƽ��ֱ������ϵ�У�˫����y=$\frac{1}{x}$��һ�κ���y=kx+b��k��0���ֱ��ڵ�A���B��ֱ����y�ύ�ڵ�C����ֱ��AB���ŵ�C��תһ���ĽǶȺõ�һ����ֱ�ߣ�����ֱ����˫����y=-$\frac{1}{x}$�ཻ�ڵ�E��F����ʹ��˫����y=$\frac{1}{x}$��y=-$\frac{1}{x}$������y=kx+b�Լ���ֱ�߹��ɵ�ͼ���ܹ���ij��������Գƣ������A�ĺ�����Ϊ1����kΪ����ʱ����A����E����B����F���ɵ��ı��ε������С����Сֵ�Ƕ��٣� ���� ��A��������뷴����y=$\frac{1}{x}$�У����y��ֵȷ����A�������꣬��A�������y=kx+b�б�ʾ��b���õ�һ�κ�������ʽ���뷴��������ʽ��������ȥy�õ�����x��һԪ���η��̣�������̵Ľ��ʾ��B���꣬��˫����y=$\frac{1}{x}$��y=-$\frac{1}{x}$��ֱ��y=kx+b�Լ���ֱ�ߵĶԳ��Կɵã���A���E����y��Գƣ���B���F����y��Գƣ���ʾ��E��F���꣬����ȷ����AE��BF����AE��BF�ľ���Ϊk+1���������ε������ʽ��ʾ������AEBF��������ɣ�
��� 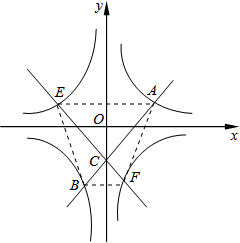 �⣺��xA=1��A����y=$\frac{1}{x}$�ϣ�
�⣺��xA=1��A����y=$\frac{1}{x}$�ϣ�
��yA=1��
�ѵ�A��1��1������y=kx+b�еã�1=k+b��
��b=1-k��
��y=kx+��1-k����
��$\left\{\begin{array}{l}{y=\frac{1}{x}}\\{y=kx+��1-k��}\end{array}\right.$����ȥy�ã�$\frac{1}{x}$=kx+��1-k����
�����ã�kx2+��1-k��x-1=0��
��x1=1��x2=-$\frac{1}{k}$��
���B��������-$\frac{1}{k}$��-k����
��˫����y=$\frac{1}{x}$��y=-$\frac{1}{x}$��ֱ��y=kx+b�Լ���ֱ�ߵĶԳ��Կɵã�
��A���E����y��Գƣ���B���F����y��Գƣ�
��E��-1��1����F��$\frac{1}{k}$��-k����
��AE=2��BF=$\frac{2}{k}$��AE��BF�ľ���Ϊk+1��
��S����AEBF=$\frac{2+\frac{2}{k}}{2}$��k+1��=��1+$\frac{1}{k}$����k+1��=k+$\frac{1}{k}$+2��
��k��0�൱k=1ʱ������SAEBF����Сֵ4��
���� �������ڷ����������ۺ��⣬�漰��֪ʶ�У�����ϵ����ȷ����������ʽ��һ�κ����뷴���������Ľ��㣬������ͼ�����ʣ��Լ��ԳƵ����ʣ���˫����y=$\frac{1}{x}$��y=-$\frac{1}{x}$��ֱ��y=kx+b�Լ���ֱ�ߵĶԳ��Կɵã���A���E����y��Գƣ���B���F����y��Գ��ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ��Ⱥ���ʡ���꼶�ڶ����¿���ѧ�Ծ��������棩 ���ͣ���ѡ��
һ��������װ��6������3��������Щ�����ɫ�⣬��״����С���ʵص���ȫ��ͬ. �ڿ�������������£�����ش��������������һ������������ĸ���Ϊ�� ��
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��?ABCD�У�EΪAD�����ȷֵ㣬����BE����AC�ڵ�F����D��BE��ƽ���߽�AC��G����BC��M��AC=12����FGΪ2.4��6��
��?ABCD�У�EΪAD�����ȷֵ㣬����BE����AC�ڵ�F����D��BE��ƽ���߽�AC��G����BC��M��AC=12����FGΪ2.4��6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��a-9�� | B�� | ��a-3����a+3�� | C�� | ��a-3a����a+3a�� | D�� | ��a-3��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 һ�κ���y=��m+2��x+��1+m����ͼ����ͼ��ʾ����m��ȡֵ��Χ�ǣ�������
һ�κ���y=��m+2��x+��1+m����ͼ����ͼ��ʾ����m��ȡֵ��Χ�ǣ�������| A�� | m��-1 | B�� | m��-2 | C�� | -2��m��-1 | D�� | m��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
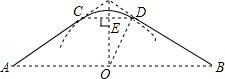 ��ͼ��ij����һ����һ���ƺ����Ӱ���֣���ʵ�߲������ز�ƺ��Χ��һ��С·��С·��������ȵ��߶�AC��BD��Բ��CD��ɣ�����AC��BD�ֱ���Բ��CD�����ڵ�C��D�������������߶�CD��뾶OD��Ϊ60�ף�������С·�ij���Ϊ120$\sqrt{3}$+2���ף�
��ͼ��ij����һ����һ���ƺ����Ӱ���֣���ʵ�߲������ز�ƺ��Χ��һ��С·��С·��������ȵ��߶�AC��BD��Բ��CD��ɣ�����AC��BD�ֱ���Բ��CD�����ڵ�C��D�������������߶�CD��뾶OD��Ϊ60�ף�������С·�ij���Ϊ120$\sqrt{3}$+2���ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �ɼ�����ͬ��С�����������һ�������壬�ü����������ͼ��ͼ��ʾ����ü��������Ϊ��������
�ɼ�����ͬ��С�����������һ�������壬�ü����������ͼ��ͼ��ʾ����ü��������Ϊ��������| A�� |  | B�� |  | C�� | 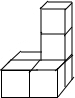 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���ABC=90�㣬BC=1����Rt��ABC�Ƶ�C˳ʱ����ת60�㣬��ʱ��Bǡ����DE�ϣ����е�A������·��Ϊ��AD����ͼ����Ӱ���ֵ������$\frac{��}{2}$-$\frac{\sqrt{3}}{4}$��
��ͼ����Rt��ABC�У���ABC=90�㣬BC=1����Rt��ABC�Ƶ�C˳ʱ����ת60�㣬��ʱ��Bǡ����DE�ϣ����е�A������·��Ϊ��AD����ͼ����Ӱ���ֵ������$\frac{��}{2}$-$\frac{\sqrt{3}}{4}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com