
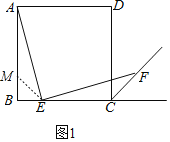
【题目】已知四边形ABCD是正方形,点E是边BC上的任意一点,AE⊥EF,且直线EF交正方形外角的平分线CF于点F.
(1)如图1,求证:AE=EF;
(2)如图2,当AB=2,点E是边BC的中点时,请直接写出FC的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)截取BE=BM,连接EM,求出AM=EC,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可;
(2)取AB中点M,连接EM,求出BM=BE,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可.
(1)证明:如图1,在AB上截取BM=BE,连接ME,
∵∠B=90°,
∴∠BME=∠BEM=45°,
∴∠AME=135°
∵CF是正方形的∠C外角的平分线,
∴∠ECF=90°+45°=135°
∴∠AME=∠ECF,
∵AB=BC,BM=BE,
∴AM=EC,
∵AE⊥EF,
∴∠AEF=90°,
∴∠AEB+∠CEF=90°,
∵∠BAE+∠AEB=90°,
∴∠BAE=∠CEF,
在△AME和△ECF中
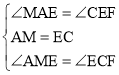 ,
,
∴△AME≌△ECF(ASA),
∴AE=EF;
(2)解:取AB中点M,连接EM,
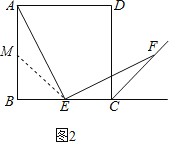
∵AB=BC,E为BC中点,M为AB中点,
∴AM=CE=BE,
∴∠BME=∠BME=45°,
∴∠AME=135°=∠ECF,
∵∠B=90°,
∴∠BAE+∠AEB=90°,
∵∠AEF=90°,
∴∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
在△AME和△ECF中
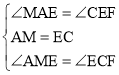 ,
,
∴△AME≌△ECF(ASA),
∴EM=CF,
∵AB=2,点E是边BC的中点,
∴BM=BE=1,
∴CF=ME=![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
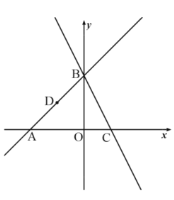
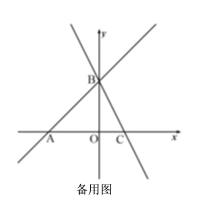
【题目】如图,![]() ,
,![]() 是直线
是直线![]() 与坐标轴的交点,直线
与坐标轴的交点,直线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() ,
,![]() ,
,![]() 三点的坐标.
三点的坐标.
(2)当点![]() 是
是![]() 的中点时,在
的中点时,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的和最小,画出点
的和最小,画出点![]() 的位置,并求
的位置,并求![]() 点的坐标.
点的坐标.
(3)若点![]() 是折线
是折线![]() 上一动点,是否存在点
上一动点,是否存在点![]() ,使
,使![]() 为直角三角形,若存在,直接写出
为直角三角形,若存在,直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
材料![]() .若一元二次方程
.若一元二次方程 ![]() 的两根为
的两根为 ![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
材料![]() .已知实数
.已知实数 ![]() ,
,![]() 满足
满足 ![]() ,
,![]() ,且
,且 ![]() ,求
,求![]() 的值.
的值.
解:由题知 ![]() ,
,![]() 是方程
是方程 ![]() 的两个不相等的实数根,
的两个不相等的实数根,
根据材料 ![]() 得
得 ![]() ,
,![]() ,
,
∴![]() .
.
解决问题:
(1)一元二次方程 ![]() 的两根为
的两根为 ![]() ,
,![]() ,则
,则 ![]() ,
,![]() .
.
(2)已知实数 ![]() ,
,![]() 满足
满足 ![]() ,
,![]() ,且
,且![]() ,求
,求
![]() 的值.
的值.
(3)已知实数 ![]() ,
,![]() 满足
满足 ![]() ,
,![]() ,且
,且 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向。为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行多少小时即可到达? (结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
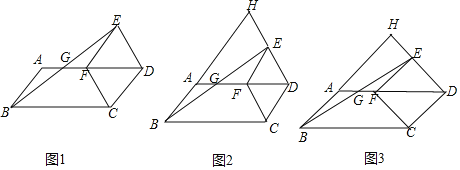
【题目】如图1,以□ABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上,连接BE,交AF于点G.
(1)猜想BG与EG的数量关系.并说明理由;
(2)延长DE,BA交于点H,其他条件不变,
①如图2,若∠ADC=60°,求![]() 的值;
的值;
②如图3,若∠ADC=α(0°<α<90°),直接写出![]() 的值.(用含α的三角函数表示)
的值.(用含α的三角函数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:梯形ABCD中,AD∥BC,∠ABC=90°,AD=4, AB=3,![]() ,在线段BC上取一点P(不与B、C重合),联结DP,作射线PQ⊥DP,PQ与直线AB交于点Q.
,在线段BC上取一点P(不与B、C重合),联结DP,作射线PQ⊥DP,PQ与直线AB交于点Q.
(1)求出梯形ABCD的面积;
(2)若点Q在边AB上,设CP=x,AQ=y,试写出y关于自变量x的函数关系式,并写出定义域.
(3)△DPC是等腰三角形,求AQ的长.
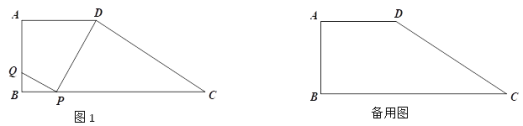
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标都在格点上,且△A1B1C1与△ABC关于原点O成中心对称,C点坐标为(-2,1)。
(1)请直接写出A1的坐标 ;并画出△A1B1C1.
(2)P(a,b)是△ABC的AC边上一点,将△ABC平移后点P的对称点P'(a+2,b﹣6),请画出平移后的△A2B2C2.
(3)若△A1B1C1和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com