
【题目】如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是_________________。
【答案】![]()
【解析】
首先连接EF交AC于O,由矩形ABCD中,四边形EGFH是菱形,易证得△CFO≌△AOE(AAS),即可得OA=OC,然后由勾股定理求得AC的长,继而求得OA的长,又由△AOE∽△ABC,利用相似三角形的对应边成比例,即可求得答案.
连接EF交AC于O,
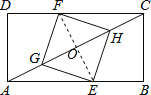
∵四边形EGFH是菱形,
∴EF⊥AC,OE=OF,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO与△AOE中,
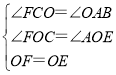 ,
,
∴△CFO≌△AOE(AAS),
∴AO=CO,
∵AC=![]() ,
,
∴AO=![]() AC=5,
AC=5,
∵∠CAB=∠CAB,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() .
.
故答案为: ![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
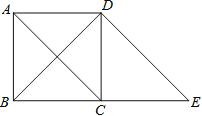
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经销一种商品,已知其每件进价为40元。现在每件售价为70元,每星期可卖出500件。该商场通过市场调查发现:若每件涨价1元,则每星期少卖出10件;若每件降价1元,则每星期多卖出m(m为正整数)件。设调查价格后每星期的销售利润为W元。
(1)设该商品每件涨价x(x为正整数)元,
①若x=5,则每星期可卖出____件,每星期的销售利润为_____元;
②当x为何值时,W最大,W的最大值是多少。
(2)设该商品每件降价y(y为正整数)元,
①写出W与Y的函数关系式,并通过计算判断:当m=10时每星期销售利润能否达到(1)中W的最大值;
②若使y=10时,每星期的销售利润W最大,直接写出W的最大值为_____。
(3)若每件降价5元时的每星期销售利润,不低于每件涨价15元时的每星期销售利润,求m的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(2,0),B(6,0),CB⊥x轴于点B,连接AC
画图操作:
(1)在y正半轴上求作点P,使得∠APB=∠ACB(尺规作图,保留作图痕迹)
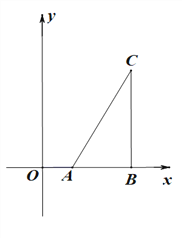
理解应用:
(2)在(1)的条件下,
①若tan∠APB ![]() ,求点P的坐标
,求点P的坐标
②当点P的坐标为 时,∠APB最大
拓展延伸:
(3)若在直线y![]() x+4上存在点P,使得∠APB最大,求点P的坐标
x+4上存在点P,使得∠APB最大,求点P的坐标
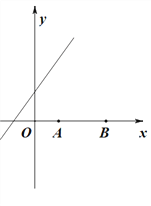
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为⊙O的内接三角形,BC=24 , ![]() ,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
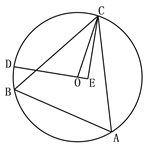
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民小胡上星期五以每股13.1元的价格买进某种股票1000股,该股票本周的涨跌情况(表格数字表示比前--天涨或跌多少元)如下表(单位:元):
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | -0.3 | 0 | -0.1 | +0.2 | +0.1 |
(1)本周内最高价是每股__________元最低价是每股元_________;
(2)如果小胡在星期五收盘前将全部股票卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如![]() 就是完全对称式(代数式中
就是完全对称式(代数式中![]() 换成b,b换成
换成b,b换成![]() ,代数式保持不变).下列三个代数式:①
,代数式保持不变).下列三个代数式:①![]() ;②
;②![]() ;③
;③![]() .其中是完全对称式的是( )
.其中是完全对称式的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com