
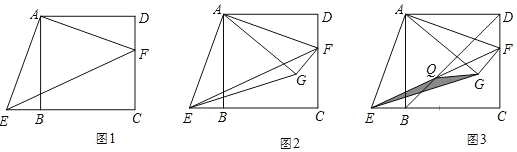
【题目】已知,在正方形 ABCD 中,AB=5,点 F 是边 DC 上的一个动点,将△ADF 绕点 A 顺时针旋转 90°至△ABE,点 F 的对应点 E 落在 CB 的延长线上,连接 EF.
(1)如图 1,求证:∠DAF+∠FEC=∠AEF;
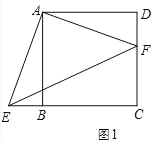
(2)将△ADF 沿 AF 翻折至△AGF,连接 EG.
①如图 2,若 DF=2,求 EG 的长;
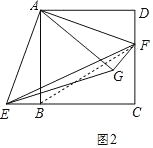
②如图 3,连接 BD 交 EF 于点 Q,连接 GQ,则 S△QEG 的最大值为 .
【答案】(1)证明见解析;(2)①EG=![]() ;②
;②![]() .
.
【解析】
(1)由∠DAF+∠EAF+∠AEF+∠FEC=180°,∠DAF+∠FEC=45°,可推出结果;
(2)①连接 BF, 证出△AEG≌△AFB(SAS),即可根据勾股定理求出EG;②作 FH⊥CD 交 BD 于 H,QM⊥BC 于 M,连接 BF,BG,设BF 交 EG 于点 O,证出△EFG≌△FEB(SSS),设 DF=EB=x,再证出△FHQ≌△EBQ(AAS),列出含x的面积公式,利用二次函数配方即可得到最大值.
证明:如图 1 中,
∵四边形 ABCD 是正方形,
∴AD∥BC,∴∠DAE+∠AEC=180°,
∵△ABE 是由△ADF 绕点 A 顺时针旋转 90°得到,
∴∠EAF=90°,AE=AF,
∴∠AEF=45°,
∴∠DAF+∠EAF+∠AEF+∠FEC=180°,
∴∠DAF+∠FEC=45°,
∴∠DAF+∠FEC=∠AEF.
①如图 2 中,连接 BF.
∵四边形 ABCD 是正方形,
∴AB=BC=CD=5,∠C=90°,
∵DF=2,
∴CF=3,
∵∠DAF=∠FAG=∠BAE,
∴∠EAG=∠FAB,
∵AE=AF,AG=AB,
∴△AEG≌△AFB(SAS),
∴EG=BF,
在 Rt△BCF 中,BF=![]() =
=![]() ,
,
∴EG=BF= ![]() .
.
②如图 3 中,作 FH⊥CD 交 BD 于 H,QM⊥BC 于 M,连接 BF,BG,设
BF 交 EG 于点 O.
∵EG=BF,BF=FB,FG=EB,
∴△EFG≌△FEB(SSS),
∴∠GEF=∠EFB,
同法可证∠FBG=∠EGB,
∵∠EOF=∠BOG,
∴∠EFB=∠FBG,
∴EF∥BG,
∴S△EQG=S△EBQ,设 DF=EB=x,则 CF=5﹣x,
∵FH∥BE,FH=DF=EB,
∴∠FHQ=∠EBQ,
∵∠HQF=∠EQB,
∴△FHQ≌△EBQ(AAS),
∴FQ=EQ,
∵QM∥CF,
∴EM=MC,
∴QM=![]() CF=
CF=![]() (5﹣x),
(5﹣x),
∴S△EQG=S△E BQ=![]() x
x ![]() (5﹣x)=﹣
(5﹣x)=﹣ ![]() (x2﹣5x)=﹣
(x2﹣5x)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣![]() <0,
<0,
∴x= ![]() 时,△EQG 的面积最大,最大值为
时,△EQG 的面积最大,最大值为![]() , 故答案为
, 故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】某中学形展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.

(1)根据图示填写下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 | ||
九(2) | 85 | 100 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司营销A,B两种产品,根据市场调研,发现如下信息:
信息1:销售A种产品所获利润y(万元)与所售产品x(吨)之间存在二次函数关系![]() 。
。
当x=1时,y=1.4;当x=3时,y=3.6。
信息2:销售B种产品所获利润y(万元)与所售产品x(吨)之间存在正比例函数关系![]() 。
。
根据以上信息,解答下列问题:
(1)求二次函数解析式;
(2)该公司准备购进A,B两种产品共10吨,请设计一个营销方案,使销售A,B两种产品获得的利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
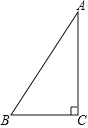
【题目】如图,△ABC 中,∠C=90°,将△ABC 绕点 C 顺时针旋转 90°,得到△DEC(其中点 D、E 分别是 A、B 两点旋转后的对应点).
(1)请画出旋转后的△DEC;
(2)试判断 DE 与 AB 的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
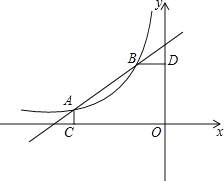
【题目】如图,在平面直角坐标系中,直线y=![]() x+
x+![]() 与反比例函数y=
与反比例函数y=![]() (x<0)的图象交于A(-4,a)、B(-1,b)两点,AC⊥x轴于C,BD⊥y轴于D.
(x<0)的图象交于A(-4,a)、B(-1,b)两点,AC⊥x轴于C,BD⊥y轴于D.
(1)求a 、b及k的值;
(2)连接OA,OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:

(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.
(1)求降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?
查看答案和解析>>
科目:初中数学 来源: 题型:
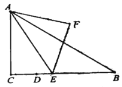
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一定点,且
边上一定点,且![]() ,点
,点![]() 是线段
是线段![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() .当点
.当点![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止时,点
停止时,点![]() 的运动的路径长为_________.
的运动的路径长为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com