

���� ��1�����ݷǸ��������ʣ��ó�����a��b�ķ����飬���a��b���ɵõ�A��B��������꣬������õ��������ε����ʵó���OAB�Ķ�����
��2����EF��y����F���������ֱ��������BEF���������E�����꣬���á�BHE��������ɵõ���E��BH�ľ��룻��G��m��n��������BEΪ��BHG�����ߣ���õ�G���꼴�ɣ�
��3������B��BK��OC����MN�ڵ�K��Ȼ��֤����OBK�ա�OAD����MKB�ա�MCB���Ӷ���֤����ADO+��BCM=180�㣮
��� �⣺��1����$\sqrt{a-b}$+��b2-16��2=0��
��a-b=0��b2-16=0��
��ã�b=4��a=4��b=-4��a=-4��
��A����x�������ᣬB����y���������ϣ�
��b=4��a=4��
��A��4��0����B��0��4����
��OA=OB=4��
���OAB=45�㣻
��2������ͼ1����EF��y����F��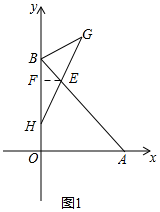
��B��0��4����H��0��1����
��BH=OB-OH=4-1=3��
��S��BHE=3��
��$\frac{1}{2}$BH��EF=3����$\frac{1}{2}$��3��EF=3��
��EF=2��
�ʵ�E��BH�ľ���Ϊ2��
�ڡ�OA=OB=4��
���OABΪ����ֱ�������Σ�
���OBA=��OAB=45�㣬
���BFEΪ����ֱ�������Σ�
��BF=EF=2��
��OF=OB-BF=4-2=2��
��E��2��2����
��EF=2��
��G��m��n����
��BEΪ��BHG�����ߣ�
��$\frac{m+0}{2}=2$��$\frac{n-1}{2}$+1=2��
���m=4��n=3��
��G��������4��3����
��3����ͼ2������B��BK��OC����MN�ڵ�K�����KBO=��DOA��
��MN��AD��
���DON+��NOA=90�㣬
���3+��NOA=90�㣬
�ߡ�NOA+��1=90�㣬
���3=��1��
�ڡ�KOB�͡�OAD�У�
$\left\{\begin{array}{l}{��KBO=��DOA}\\{OA=OB}\\{��3=��1\\;}\end{array}\right.$��
���KOB�ա�OAD��ASA����
��KB=OD����2=��7��
��BC=OD��
��KB=BC��
��OB=OA����BOA=90�㣬
���OBA=45�㣬
���9=��8=45�㣬
�ڡ�MKB�͡�MCB�У�
$\left\{\begin{array}{l}{MB=MB}\\{��9=��8}\\{KB=CB}\end{array}\right.$��
���MKB�ա�MCB��SAS����
���6=��5��
�ߡ�7+��6=180�㣬
���2+��5=180�㣬����ADO+��BCM=180�㣮
���� ������Ҫ���������ε��ۺ�Ӧ�ã��������ʱ��Ҫ����������ͼ�ε����ʣ�ȫ�������ε��ж������ʣ��е����깫ʽ������ֱ�������ε������Լ������ε�����ȣ����ʱ�������߹���ȫ���������ǹؼ���


 ���ݼ���ϵ�д�
���ݼ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
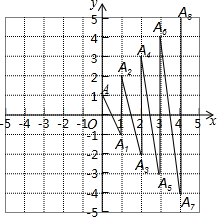 ��ͼ��ƽ��ֱ������ϵ����һ��A��0��1������A��һ����������A1��1��-1�����ڶ����ɵ� A1������A2��1��2�����������ɵ�A2����A3��2��-2�����ɴ˹���������ȥ����80��������A80�������ǣ�������
��ͼ��ƽ��ֱ������ϵ����һ��A��0��1������A��һ����������A1��1��-1�����ڶ����ɵ� A1������A2��1��2�����������ɵ�A2����A3��2��-2�����ɴ˹���������ȥ����80��������A80�������ǣ�������| A�� | ��40��40�� | B�� | ��41��40�� | C�� | ��40��41�� | D�� | ��41��41�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
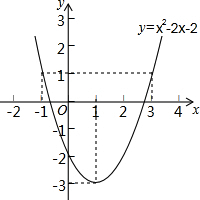 ����y=x2-2x-2��ͼ����ͼ��ʾ�����������ṩ����Ϣ�������ʹy��1������x��ȡֵ��Χ�ǣ�������
����y=x2-2x-2��ͼ����ͼ��ʾ�����������ṩ����Ϣ�������ʹy��1������x��ȡֵ��Χ�ǣ�������| A�� | -1��x��3 | B�� | -1��x��3 | C�� | x��-1��x��3 | D�� | x��-1��x��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x2��3=x5 | B�� | x2+x3=x5 | C�� | ��x-y��2��y-x��3=��x-y��5 | D�� | x2•x3=x5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У�ADΪ��BAC��ƽ���ߣ�DE��AB��E��DF��AC��F����ABC�������28cm2��AB=20cm��AC=8cm����DE�ij��ǣ�������
��ͼ���ڡ�ABC�У�ADΪ��BAC��ƽ���ߣ�DE��AB��E��DF��AC��F����ABC�������28cm2��AB=20cm��AC=8cm����DE�ij��ǣ�������| A�� | 4cm | B�� | 3cm | C�� | 2cm | D�� | 1cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��3�� | B�� | ��-2��-3�� | C�� | ��2��3�� | D�� | ��2��-3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{y}{2}$ | B�� | $\frac{1}{a-1}$ | C�� | x | D�� | $\frac{1}{3��}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com