
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
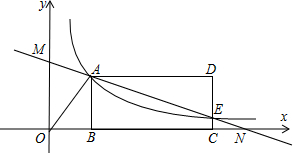 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(3,0),tan∠AOB=$\frac{4}{3}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(3,0),tan∠AOB=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
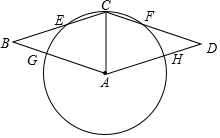 如图,菱形ABCD,以A为圆心,AC长为半径的圆分别交边BC,DC,AB,AD于点E,F,G,H.
如图,菱形ABCD,以A为圆心,AC长为半径的圆分别交边BC,DC,AB,AD于点E,F,G,H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
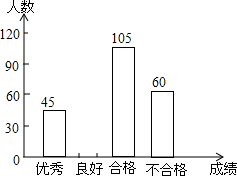 为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:| 成绩 | 频数 | 频率 |
| 优秀 | 45 | b |
| 良好 | a | 0.3 |
| 合格 | 105 | 0.35 |
| 不合格 | 60 | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
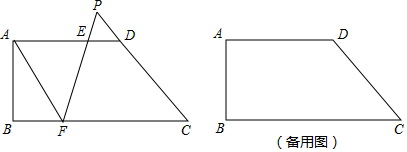
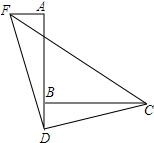 如图,已知∠ABC=90°,D是AB延长线上的点,AD=BC,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,求证:FD⊥CD.
如图,已知∠ABC=90°,D是AB延长线上的点,AD=BC,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,求证:FD⊥CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com