
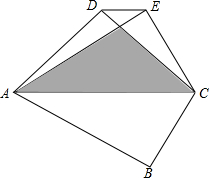
 如图,由一副三角板组成的四边形ABCD中,∠B=∠ADC=90°,∠BAC=30°,把△ABC沿AC折叠,点B落在点E处,若两个三角形重叠部分的面积为2$\sqrt{3}$+2,则DE=$\sqrt{2}$.
如图,由一副三角板组成的四边形ABCD中,∠B=∠ADC=90°,∠BAC=30°,把△ABC沿AC折叠,点B落在点E处,若两个三角形重叠部分的面积为2$\sqrt{3}$+2,则DE=$\sqrt{2}$. 分析 过D点作DE⊥AC于E,过O点作OF⊥AC于F,过E作EH⊥DE于H,连接EB交AC于G.
解答 解:过D点作DE⊥AC于E,过O点作OF⊥AC于F,过E作EH⊥DE于H,连接EB交AC于G.
∵AE=AB,EC=BC,
∴BE⊥AC,
∵∠OFC=90°,∠OCF=45°,
∴∠OCF=∠FOC=45°,
∴OF=FC,设OF=FC=x,则AF=$\sqrt{3}$x,
∴S△AOC=2$\sqrt{3}$+2,
∴$\frac{1}{2}$•($\sqrt{3}$x+x)•x=2$\sqrt{3}$+2,
∵x>0,
∴x=2,
∴AC=2+2$\sqrt{3}$,EC=$\frac{1}{2}$AC=1+$\sqrt{3}$,AE=$\sqrt{3}$EC=3+$\sqrt{3}$,GC=$\frac{1}{2}$EC=$\frac{1}{2}$(1+$\sqrt{3}$),EG=$\frac{\sqrt{3}}{2}$(1+$\sqrt{3}$),
∵DE⊥AC,AD=DC,∠ADC=90°,
∴DE=EC=$\frac{1}{2}$AC=1+$\sqrt{3}$,
∵EG=$\frac{1}{2}$AE=$\frac{1}{2}$(3+$\sqrt{3}$),
∴EG=HE=$\frac{1}{2}$(3+$\sqrt{3}$),HE=EG=EC-GC=$\frac{1}{2}$(1+$\sqrt{3}$),
∴DH=$\frac{1}{2}$($\sqrt{3}$-1)
∴DE=$\sqrt{D{H}^{2}+H{E}^{2}}$=$\sqrt{[\frac{1}{2}(\sqrt{3}-1)]^{2}+[\frac{1}{2}(\sqrt{3}+1)]^{2}}$=$\sqrt{2}$.
故答案为$\sqrt{2}$.
点评 本题考查翻折变换、等腰直角三角形的性质,30度的直角三角形的性质、勾股定理等知识,解题的关键是熟练应用这些知识解决问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:填空题
 已知?ABCD,连结对角线BD,E、F是边BC的三等分点,连结AE、AF,与BD分别交于点G、H,则BG:GH:HD的值为5:3:12.
已知?ABCD,连结对角线BD,E、F是边BC的三等分点,连结AE、AF,与BD分别交于点G、H,则BG:GH:HD的值为5:3:12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由5x-7y=2,得-2-7y=5x | B. | 由6x-3=x+4,得6x-3=4+x | ||
| C. | 由8-x=x-5,得-x-x=-5-8 | D. | 由x+9=3x-1,得3x-1=x+9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com