
| A. | $\frac{276}{35}$ | B. | -$\frac{276}{35}$ | C. | $\frac{11}{12}$ | D. | -$\frac{11}{12}$ |
分析 已知等式变形,整理求出$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$的值,进而确定出x,y,z的值,即可求出x+y+z的值.
解答 解:由题意得:$\frac{xy}{x+y}$=1,$\frac{yz}{y+z}$=2,$\frac{zx}{z+x}$=3,即$\frac{1}{x}$+$\frac{1}{y}$=1,$\frac{1}{y}$+$\frac{1}{z}$=$\frac{1}{2}$,$\frac{1}{x}$+$\frac{1}{z}$=$\frac{1}{3}$,
∴2($\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$)=$\frac{11}{6}$,即$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$=$\frac{11}{12}$,
∴$\frac{1}{x}$=$\frac{5}{12}$,$\frac{1}{y}$=$\frac{7}{12}$,$\frac{1}{z}$=-$\frac{1}{12}$,
即x=$\frac{12}{5}$,y=$\frac{12}{7}$,z=-12,
则x+y+z=$\frac{12}{5}$+$\frac{12}{7}$-12=-$\frac{276}{35}$.
故选:B.
点评 此题考查了比例的性质,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$是无理数 | B. | 3<$\sqrt{12}$<4 | ||
| C. | $\sqrt{12}$是12的算术平方根 | D. | $\sqrt{12}$不能化简 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
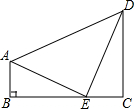 在四边形ABCD中,AB∥CD,∠B=∠C=90°,E是BC上一点,连接AE,DE,且∠AED=90°,AB=CE,求证:E在AD的中垂线上.
在四边形ABCD中,AB∥CD,∠B=∠C=90°,E是BC上一点,连接AE,DE,且∠AED=90°,AB=CE,求证:E在AD的中垂线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com