
【题目】两个完全相同的正四面体骰子的各面上分别标明数字1,2,3,4,在桌子上同时投掷这两个正四面体骰子,请用列表法或画树状图的方法,求与桌面接触的面所得的点数之和等于6的概率.
【答案】![]()
【解析】试题分析:
如果采用列表法,那么可以将每枚骰子可能出现的点数分别在纵横两个方向上依次列出,并按照表格的结构依次填写各种可能的组合情况. 如果采用树状图法,那么可以将第一枚骰子的情况作为第一层,第二枚骰子的情况作为第二层,先在第一层上列出可能出现的点数,再根据树状图的特点和第二枚骰子可能出现的点数完成第二层. 分析上述的表或树状图,统计所有可能的情况以及所求事件的可能情况的数量,利用概率计算公式求得相应的概率.
试题解析:
(1) (列表法)
根据题意列表如下.
第一枚骰子 第二枚骰子 | 1 | 2 | 3 | 4 |
1 | (1, 1) | (2, 1) | (3, 1) | (4, 1) |
2 | (1, 2) | (2, 2) | (3, 2) | (4, 2) |
3 | (1, 3) | (2, 3) | (3, 3) | (4, 3) |
4 | (1, 4) | (2, 4) | (3, 4) | (4, 4) |
由上表可以看出,共有16种情况,其中两个骰子与桌面接触的面所得的点数之和等于6的情况共有3种.
∴P(与桌面接触的面所得的点数之和等于6)= ![]() .
.
(2) (树状图法)
根据题意画出如下图所示的树状图.
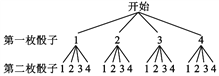
由上面的树状图可以看出,共有16种情况,其中两个骰子与桌面接触的面所得的点数之和等于6的情况共有3种.
∴P(与桌面接触的面所得的点数之和等于6)= ![]() .
.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中, ![]() =8
=8![]() ,
, ![]() =6
=6![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以2
以2 ![]() 的速度向终点
的速度向终点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() →
→![]() 以4
以4 ![]() 的速度向点
的速度向点![]() 匀速运动,到达点
匀速运动,到达点![]() 后,继续沿
后,继续沿![]() →
→![]() 以3
以3 ![]() 的速度向终点
的速度向终点![]() 匀速运动.连结
匀速运动.连结![]() ,以
,以![]() 、
、![]() 为边作□
为边作□![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (
(![]() ),□
),□![]() 与矩形
与矩形![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() .
.
(1)当点![]() 在点
在点![]() 上,△
上,△![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的值.
的值.
(2)当点![]() 在边
在边![]() 上,△
上,△![]() 与△
与△![]() 相似时,求
相似时,求![]() 的值.
的值.
(3)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当△![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【感知】如图①,在Rt△ABC中,∠C=90°,AC=BC,点D、E分别在边AC、BC上,且DE∥AB,易证AD=BE(不需要证明).
【探究】连结图①中的AE,点M、N、P分别为DE、AE、AB的中点,顺次连结M、N、P,其它条件不变,如图②,求证:△MNP是等腰直角三角形.
【应用】将图②中的点D、E分别移动到AC、BC的延长线上,其它条件不变,在连结BD,并取其中点Q,顺次连结M、N、P、Q,如图③,若![]() =
=![]() ,且DE=
,且DE=![]() ,则四边形MNPQ的面积为 .
,则四边形MNPQ的面积为 .



查看答案和解析>>
科目:初中数学 来源: 题型:
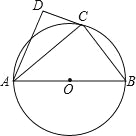
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.

(1)如图①所示,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(至少说出两种): 或者 .
(2)如图②所示,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一个数比它的相反数大-4”,若设这数是x,则可列出关于x的方程为( ).
A.x=-x+4
B.x=-x+(-4)
C.x=-x-(-4)
D.x-(-x)=4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com