
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a﹣2|+(b﹣3)2=0.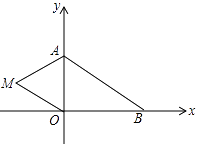
(1)a= , b=;
(2)如果在第二象限内有一点M(m,1),请用含m的式子表示四边形ABOM的面积;
(3)在(2)条件下,当m=﹣ ![]() 时,在坐标轴的负半轴上求点N(的坐标),使得△ABN的面积与四边形ABOM的面积相等.(直接写出答案)
时,在坐标轴的负半轴上求点N(的坐标),使得△ABN的面积与四边形ABOM的面积相等.(直接写出答案)
【答案】
(1)2,3
(2)解:∵在第二象限内有一点M(m,1),
∴S△AMO= ![]() ×AO×(﹣m)=﹣m,
×AO×(﹣m)=﹣m,
S△AOB= ![]() ×AO×OB=3,
×AO×OB=3,
∴四边形ABOM的面积为:3﹣m;
(3)解:∵当m=﹣ ![]() 时,△ABN的面积与四边形ABOM的面积相等,
时,△ABN的面积与四边形ABOM的面积相等,
当N在x轴的负半轴时,设N点坐标为:(c,0),
则 ![]() ×2(3﹣c)=3﹣(﹣
×2(3﹣c)=3﹣(﹣ ![]() ),
),
解得:c=﹣1.5,
故N(﹣1.5,0),
当N在y轴的负半轴时,设N点坐标为:(0,d),
则 ![]() ×3(2﹣d)=3﹣(﹣
×3(2﹣d)=3﹣(﹣ ![]() ),
),
解得:d=﹣1,
故N(0,﹣1),
综上所述:N点坐标为:(﹣1.5,0),(0,﹣1).
【解析】解:(1)∵|a﹣2|+(b﹣3)2=0,
∴a﹣2=0,b﹣3=0,
解得:a=2,b=3,
所以答案是:2,3;


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】某厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级所有学生参加2011年初中毕业英语口语、听力自动化考试,我们从中随机抽取了部分学生的考试成绩,将他们的成绩进行统计后分为A、B、C、D四等,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题: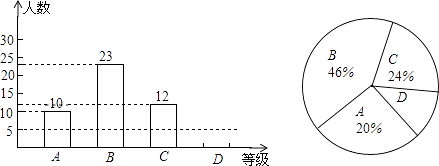
(说明:A级:25分~30分;B级:20分~24分;C级:15分~19分;D级:15分以下)
(1)请把条形统计图补充完整;
(2)扇形统计图中D级所占的百分比是;
(3)扇形统计图中A级所在的扇形的圆心角度数是;
(4)若该校九年级有850名学生,请你估计全年级A级和B级的学生人数共约为人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人体中红细胞的直径约为0.0000077m,将数0.0000077m用科学记数法表示为( )
A. 7.7×10-6 B. 0.77×10-7 C. 77×10-5 D. 7.7×10-7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F,使得AF=AE,连接DF:
(1)旋转△ADF可得到哪个三角形?
(2)旋转中心是哪一点?旋转了多少度?
(3)BE与DF的数量关系、位置关系如何?为什么?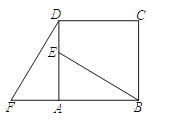
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知☉O上两个定点A、B和两个动点C、D,AC与BD交于点E。
(1)如图1,求证EA·EC=EB·ED
(2)如图2,若弧AB=弧BC,AD是☉O的直径,求证;AD·AC=2BD·BC
(3)如图3,若AC上BD,BC=3,求点0到弦AD的距离。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P,点Q分别代表两个小区,直线l代表两个小区中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站点.
①若考虑到小区P居住的老年人较多,计划建一个离小区P最近的车站,请在公路l上画出车站的位置(用点M表示);
②若考虑到修路的费用问题,希望车站的位置到小区P和小区Q的距离之和最小,请在公路l上画出车站的位置(用点N表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中必然事件有( )
A.打开电视机,正播放新闻
B.通过长期努力学习,你会成为数学家
C.从一副扑克牌中任意抽取一张牌,花色是红桃
D.某校在同一年出生的有367名学生,则至少有两人的生日是同一天
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com