
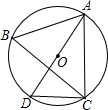
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$, 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
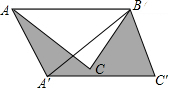 如图,在△ABC中,AB=6cm,∠CAB=45°,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为9$\sqrt{2}$cm2.
如图,在△ABC中,AB=6cm,∠CAB=45°,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为9$\sqrt{2}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
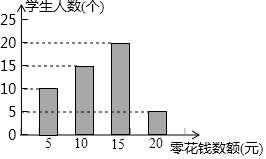 某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示.
某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
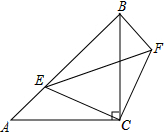 已知:如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上.
已知:如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售量p(件) | P=45-x |
| 销售单价q(元/件) | 当1≤x≤18时,q=20+x 当18<x≤30时,q=38 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com