
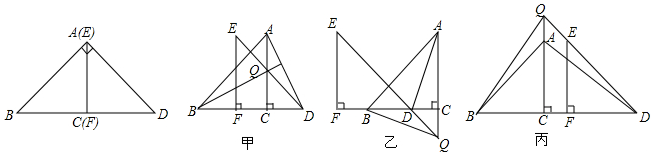
分析 (1)利用等腰直角三角形的性质结合全等三角形的判定与性质得出BQ=AD,BQ⊥AD;
(2)利用已知条件分类得出,体现数学中的分类讨论思想.
解答 解:(1)成立,
理由:如图乙:由题意可得:∠FDE=∠QDC=∠ABC=∠BAC=45°,
则DC=QC,AC=BC,
在△ADC和△BQC中
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCQ}\\{DC=CQ}\end{array}\right.$,
∴△ADC≌△BQC(SAS),
∴AD=BQ,∠DAC=∠QBC,
延长AD交BQ于点F,
则∠ADC=∠BDF,
∴∠BFD=∠ACD=90°,
∴AD⊥BQ;
(2)小慧思考问题的方式中,蕴含的数学思想是:分类讨论思想;
故答案是:分类讨论思想.
点评 此题主要考查了几何变换综合题,以及全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解题的关键.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:解答题
 已知在平面直角坐标系中,四边形OABC的四个顶点坐标分别是O(0,0),A(0,3),B(5,4),C(4,0).
已知在平面直角坐标系中,四边形OABC的四个顶点坐标分别是O(0,0),A(0,3),B(5,4),C(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
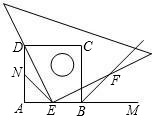 如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.
如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
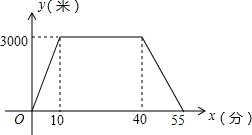 娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程y(m)和所经过的时间x(min)之间的函数图象如图所示,则下列说法不正确的是( )
娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程y(m)和所经过的时间x(min)之间的函数图象如图所示,则下列说法不正确的是( )| A. | 娟娟同学与超市相距3000m | |
| B. | 娟娟同学去超市途中的速度是300m/min | |
| C. | 娟娟同学在超市逗留了30min | |
| D. | 娟娟同学从超市返回家比从家里去超市的速度快 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
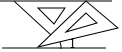 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )| A. | 30° | B. | 20° | C. | 15° | D. | 14° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com