【答案】
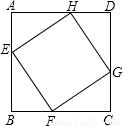
分析:(1)由于四点的运动时间和速度都相同,因此AE=BF=CG=DH,BE=CF=GH=AH由此可得出正方形四个角的直角三角形都全等,那么可根据得出的边相等先得出四边形EHGF是菱形,然后根据得出的角相等,得出四边形EHGF的内角是90°,以此来得出四边形EFGH是正方形.
(2)求正方形的面积也就是求正方形边长的平方,正方形EFGH的边长正好是四角小直角三角形的斜边,那么可用勾股定理用直角三角形的两个直角边来表示出正方形EFGH的边长的平方,已知了E点的速度,可用时间表示出AE,BE由①中的全等三角形可知,BE=AH,于是可用含t的式子表示出正方形边长的平方,也就得出了S与t的函数关系式.
(3)有大正方形的边长,就可以求出大正方形的面积,然后用(2)中得出的正方形EFGH的面积函数关系式等于大正方形面积的

,即可得出此时t的值.
解答:解:(1)∵点E,F,G,H在四条边上的运动速度相同,

∴AE=BF=CG=DH,
在正方形ABCD中,∠A=∠B=∠C=∠D=90°,
且AB=BC=CD=DA,
∴EB=FC=GD=HA,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=HG(全等三角形的对应边相等),
∠AEH=∠BFE(全等三角形的对应角相等),
∴四边形EFGH是菱形.(四条边相等的四边形是菱形),
又∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠FEH=180°-(∠BEF+∠AEH)=90°,
∴四边形EFGH为正方形.(有一个角是直角的菱形是正方形).
(2)∵运动时间为t(s),运动速度为1cm/s,
∴AE=tcm,AH=(4-t)cm,
由(1)知四边形EFGH为正方形,
∴S=EH
2=AE
2+AH
2=t
2+(4-t)
2即S=2t
2-8t+16=2(t-2)
2+8,
当t=2秒时,S有最小值,最小值是8cm
2;
(3)存在某一时刻t,使四边形EFGH的面积与正方形ABCD的面积比是5:8.
∵S=

S
正方形ABCD,
∴2(t-2)
2+8=

×16,∴t
1=1,t
2=3;
当t=1或3时,
四边形EFGH的面积与正方形ABCD的面积的比是5:8.
点评:本题主要考查了全等三角形的判定,正方形的判定与性质,二次函数的应用等知识点,用全等三角形来证得四边形EFGH是正方形是解题的关键.

 ,即可得出此时t的值.
,即可得出此时t的值.
 S正方形ABCD,
S正方形ABCD, ×16,∴t1=1,t2=3;
×16,∴t1=1,t2=3;

 名校课堂系列答案
名校课堂系列答案 的图象都过点A(m,1).
的图象都过点A(m,1).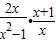 ,然后请你选取一个合适的x的值,使分式的值为一个整数.
,然后请你选取一个合适的x的值,使分式的值为一个整数.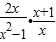 ,然后请你选取一个合适的x的值,使分式的值为一个整数.
,然后请你选取一个合适的x的值,使分式的值为一个整数.