
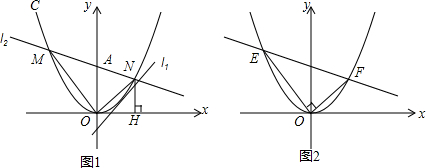
 ��ͼ����ƽ��ֱ������ϵ�У����κ���y=ax2+bx+c��a��0����ͼ��Ķ���ΪD����y�ύ�ڵ�C����x�ύ��A��B���㣬��A��ԭ�����࣬��B������Ϊ��3��0����OB=OC=3OA��
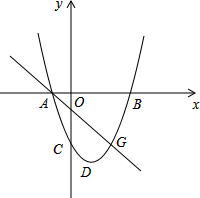
��ͼ����ƽ��ֱ������ϵ�У����κ���y=ax2+bx+c��a��0����ͼ��Ķ���ΪD����y�ύ�ڵ�C����x�ύ��A��B���㣬��A��ԭ�����࣬��B������Ϊ��3��0����OB=OC=3OA������ ��1��������֪�����������C��A�����꣬���ô���ϵ������������ߵĽ���ʽ��
��2���ɷֱ��E��G��x��Ĵ��ߣ��费��ΪF��H����ô��AGE�����=��AEF�����+�ı���FHGE�����-��AGH����������E������꣬���ɱ�ʾ��F�����꼰EF�ij��������������ó���������㷽�����ɵó����ڡ�AGE�������E�������ĺ�����ϵʽ���������ú��������ʣ����������AGE������������Ӧ��E�����ꣻ
��3�����������ߺ�Բ�ĶԳ��ԣ�֪Բ�ı��������ߵĶԳ����ϣ����ڸ�Բ��x�����У�����Բ�İ뾶��ʾ��M��N�����꣬�����������ߵĽ���ʽ�У��������Բ�İ뾶������ע�����Բ�Ŀ�����x���Ϸ���Ҳ������x���·�����Ҫ�������ۣ�
��� �⣺��1������֪�ã�C��0��-3����A��-1��0��
��A��B��C�������������$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=-3}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$
����������κ����ı���ʽΪ��y=x2-2x-3��
��2����x=2ʱ��y=x2-2x-3=-3����G��2��-3����
��AG�Ľ���ʽΪy=kx+b����A��G���뺯������ʽ����
$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=-3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$��
ֱ��AG�Ľ���ʽΪy=-x-1��
��E��EF��x�ύAG�ڣ�F��ͼ1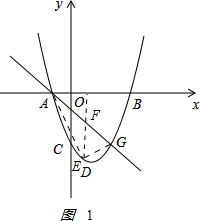 ��
��
E���������ϣ�F��ֱ��AG�ϣ�
��E��������n��n2-2n-3����F��n��-n-1����
EF=��-n-1��-��n2-2n-3��=-n2+n+2
S=$\frac{1}{2}$EF•��G-xA��=$\frac{1}{2}$����-n2+n+2��[2-��-1��]
=-$\frac{3}{2}$��n-$\frac{1}{2}$��2+$\frac{27}{8}$��
��n=$\frac{1}{2}$ʱ��S���ֵ��$\frac{27}{8}$��
n2-2n-3=-$\frac{15}{4}$����E��$\frac{1}{2}$��-$\frac{15}{4}$����
��3����ͼ2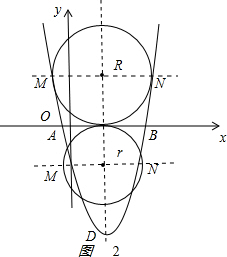 ��
��
�ٵ�ֱ��MN��x���Ϸ�ʱ����Բ�İ뾶ΪR��R��0������N��R+1��R����
���������ߵı���ʽ�����R=$\frac{1+\sqrt{17}}{2}$��
�ڵ�ֱ��MN��x���·�ʱ����Բ�İ뾶Ϊr��r��0������N��r+1��-r����
���������ߵı���ʽ�����r=$\frac{-1+\sqrt{17}}{2}$��
��Բ�İ뾶Ϊ$\frac{1+\sqrt{17}}{2}$��$\frac{-1+\sqrt{17}}{2}$��
���� ���⿼���˶��κ�������ʽ��ȷ�������ߵ����ʡ�ͼ���������֪ʶ���ۺ���ǿ������Ҫ��ϸߣ�����ѧ�����ν�ϵ���ѧ˼�뷽����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У�AD�ǡ�BAC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߣ���AD��EF�Ĺ�ϵ�ǣ�������
��ͼ���ڡ�ABC�У�AD�ǡ�BAC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߣ���AD��EF�Ĺ�ϵ�ǣ�������| A�� | EF��ֱƽ��AD | B�� | AD��ֱƽ��EF | ||
| C�� | AD��EF���ഹֱƽ�� | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 | B�� | 3 | C�� | 0 | D�� | -3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
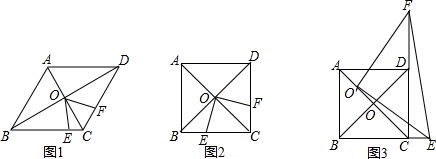
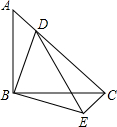 ��ͼ������Rt��ABC�У�BA=BC����ABC=90�㣬��D��AC�ϣ�����ABD�Ƶ�B��˳ʱ�뷽����ת90��õ���CBE��
��ͼ������Rt��ABC�У�BA=BC����ABC=90�㣬��D��AC�ϣ�����ABD�Ƶ�B��˳ʱ�뷽����ת90��õ���CBE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12�� | B�� | 21�� | C�� | 24�� | D�� | 42�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m=-1 | B�� | m=2 | C�� | m=3 | D�� | m=0��m=3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com