
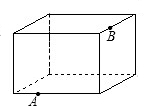
 如图,是一个长8m,宽6m,高5m的仓库,在其内壁的A(长的四等分点)处有一只壁虎,B(宽的三等分点)处有一只蚊子,则壁虎爬到蚊子处的最短距离为多少米.
如图,是一个长8m,宽6m,高5m的仓库,在其内壁的A(长的四等分点)处有一只壁虎,B(宽的三等分点)处有一只蚊子,则壁虎爬到蚊子处的最短距离为多少米. 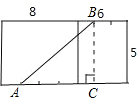 解:①将正面和左面展开,过点B向底面作垂线,垂足为点C,则△ABC为直角三角形,
解:①将正面和左面展开,过点B向底面作垂线,垂足为点C,则△ABC为直角三角形,| 3 |
| 4 |
| 1 |
| 3 |
| AC2+BC2 |
| 82+52 |
| 89 |
| 89 |
| 85 |
| 5 |
| 85 |


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
 如图是一个长8m、宽6m、高5m的仓库,在其内壁的点A(长的四等分点)处有一只壁虎、点B(宽的三等分点)处有一只蚊子.则壁虎爬到蚊子处的最短距离为
如图是一个长8m、宽6m、高5m的仓库,在其内壁的点A(长的四等分点)处有一只壁虎、点B(宽的三等分点)处有一只蚊子.则壁虎爬到蚊子处的最短距离为查看答案和解析>>
科目:初中数学 来源:2012年浙教版初中数学九年级上2.4二次函数的应用练习卷(解析版) 题型:选择题
如图所示,是一个长8m、宽6m的矩形小花园,根据需要将它的长缩短xm、宽增加xm,要想使修改后的小花园面积达到最大,则x应为( )
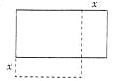
A.1m B.1.5m C.2m D.2.5m
查看答案和解析>>
科目:初中数学 来源:2009-2010学年黑龙江省八年级上期中考试数学试卷(解析版) 题型:填空题
如图是一个长8m、宽6 m、高5 m的仓库,在其内壁的点A(长的四等分点)处有一只壁虎、点B(宽的三等分点)处有一只蚊子.则壁虎爬到蚊子处的最短距离为_________________ .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com