
【题目】将一副三角板中的两块直角三角板的直角顶点![]() 按如图方式叠放在一起,友情提示:
按如图方式叠放在一起,友情提示:![]() ,
,![]() ,
,![]() .
.
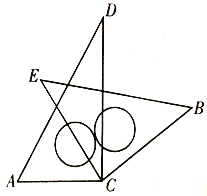
(1)①若![]() ,则
,则![]() 的度数为__________;
的度数为__________;
②若![]() ,则
,则![]() 的度数为__________.
的度数为__________.
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,当这两块角尺有一组边互相平行时,请直接写出
的上方时,当这两块角尺有一组边互相平行时,请直接写出![]() 角度所有可能的值.
角度所有可能的值.
【答案】(1)①答案为:![]() ;②答案为:
;②答案为:![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 、
、![]() .
.
【解析】
(1)①根据∠DCE和∠ACD的度数,求得∠ACE的度数,再根据∠BCE求得∠ACB的度数;②根据∠BCE和∠ACB的度数,求得∠ACE的度数,再根据∠ACD求得∠DCE的度数;
(2)根据∠ACE=90°-∠DCE以及∠ACB=∠ACE+90°,进行计算即可得出结论;
(3)分2种情况进行讨论:当CB∥AD时,当EB∥AC时,分别求得∠ACE角度即可.
解:(1)①∵∠DCE=50°,∠ACD=90°
∴∠ACE=40°
∵∠BCE=90°
∴∠ACB=90°+40°=130°
故答案为:130;
②∵∠ACB=120°,∠ECB=90°
∴∠ACE=120°-90°=30°
∴∠DCE=90°-∠ACE=90°-30°=60°
故答案为:60°;
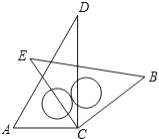
(2)猜想:![]()
理由如下:![]()
又![]()
![]()
即![]() ;
;
(3)![]() 、
、![]() ,
,
理由:当CB∥AD时,∠ACE=30°;
当EB∥AC时,∠ACE=45°.


科目:初中数学 来源: 题型:
【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点![]() 在平面直角坐标系中按图中箭头所示方向运动,第
在平面直角坐标系中按图中箭头所示方向运动,第![]() 次从原点运动到点
次从原点运动到点![]() ,第
,第![]() 次接着运动到点
次接着运动到点![]() ,第
,第![]() 次接着运动到点
次接着运动到点![]() ,
,![]() 按这样的运动规律,经过第
按这样的运动规律,经过第![]() 次运动后,动点
次运动后,动点![]() 的坐标是( )
的坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的南偏东60方向,距离灯塔100海里的A处,它计划去往位于灯塔P的北偏东45方向上的B处.(参考数据![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.449)
≈2.449)
(1)问B处距离灯塔P有多远?(结果精确到0.1海里)
(2)假设有一圆形暗礁区域,它的圆心位于射线PB上,距离灯塔190海里的点O处.圆形暗礁区域的半径为50海里,进入这个区域,就有触礁的危险.请判断海轮到达B处是否有触礁的危险,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是⊙O的直径,A是弦BD延长线上一点,切线DE平分AC于E。
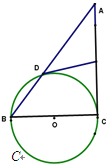
(1)求证:AC是⊙O的切线;
(2)若AD:DB=3:2,AC=15,求⊙O的直径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级去赤壁开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 30 | 42 |
租金/(元/辆) | 300 | 400 |
学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆;
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.
(1)求证:AB与⊙O相切;
(2)若等边三角形ABC的边长是8,求线段BF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com