练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    不等式组的解集是__________；



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如果二次函数的二次项系数为l，则此二次函数可表示为y=x2+px+q，我们称[p，q]为此函数的特征数，如函数y=x2+2x+3的特征数是[2，3]．

    （1）若一个函数的特征数为[﹣2，1]，求此函数图象的顶点坐标．

    （2）探究下列问题：

    ①若一个函数的特征数为[4，﹣1]，将此函数的图象先向右平移1个单位，再向上平移1个单位，求得到的图象对应的函数的特征数．

    ②若一个函数的特征数为[2，3]，问此函数的图象经过怎样的平移，才能使得到的图象对应的函数的特征数为[3，4]？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    从一栋二层楼的楼顶点A处看对面的教学楼，探测器显示，看到教学楼底部点C处的俯角为45°，看到楼顶部点D处的仰角为60°，已知两栋楼之间的水平距离为6米，则教学楼的高CD是（　　）

    　

    A．

    （6+6）米

    B．

    （6+3）米

    C．

    （6+2）米

    D．

    12米

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    等于（   ）

    A．2    B．－2    C．    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    多项式的项数及次数分别是（   ）

    A．3，3    B．3，2    C．2，3    D．2，2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个不透明的袋里有两个白球和三个红球，它们除颜色外其它都一样

    ⑴求“从袋中任意摸出一个球，摸出的一个球是白球”的概率；

    ⑵直接写出“从袋中同时任意摸出两个球，摸出的两个球都是红球”的概率；

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    我们把“按照某种理想化的要求（或实际可应用的标准）来反映或概括地表现一类或某种事物关系结构的数学形式”看作是数学中的一个“模式”（我国著名数学家徐利浩）

    如图是一个典型的图形模式，用它可以测底部可能达不到的建筑物的高度，用它可测宽，用它可解决数学中的一些问题，等等。

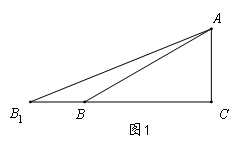
    ⑴如图1，若B1B=30米，∠B1=22°，∠ABC=30°，求AC（精确到1）；

    参考数据：sin22°≈0.37，cos22°≈0.92，tan22°≈0.40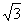，≈1.73

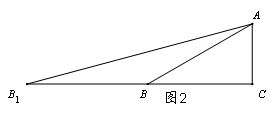
    ⑵如图2，若∠ABC=30°，B1B=AB，计算tan15°的值（保留准确值）；

    ⑶直接写出 tan7.5°的值

    注：若出现双重根式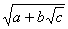，则无需化简；

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：2tan60°﹣|﹣2|﹣+（）﹣1．　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一组数据如下：3，6，7，2，3，4，3，6，那么这组数据的中位数和众数分别是

    A．3，3       B．3.5，3        C．4，3        D．3.5，6

    查看答案和解析>>

    同步练习册答案