
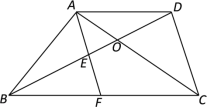
【题目】如图,在梯形ABCD中,AD//BC,AC与BD相交于点O,点E在线段OB上,AE的延长线与BC相交于点F,OD2 = OB·OE.
(1)求证:四边形AFCD是平行四边形;
(2)如果BC=BD,AE·AF=AD·BF,求证:△ABE∽△ACD.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)由题意,得到![]() ,然后由AD∥BC,得到
,然后由AD∥BC,得到![]() ,则
,则![]() ,即可得到AF//CD,即可得到结论;
,即可得到AF//CD,即可得到结论;
(2)先证明∠AED=∠BCD,得到∠AEB=∠ADC,然后证明得到![]() ,即可得到△ABE∽△ADC.
,即可得到△ABE∽△ADC.
证明:(1)∵OD2 =OE · OB,
∴![]() .
.
∵AD//BC,
∴![]() .
.
∴![]() .
.
∴ AF//CD.
∴四边形AFCD是平行四边形.
(2)∵AF//CD,
∴∠AED=∠BDC,![]() .
.
∵BC=BD,
∴BE=BF,∠BDC=∠BCD
∴∠AED=∠BCD.
∵∠AEB=180°![]() ∠AED,∠ADC=180°
∠AED,∠ADC=180°![]() ∠BCD,
∠BCD,
∴∠AEB=∠ADC.
∵AE·AF=AD·BF,
∴![]() .
.
∵四边形AFCD是平行四边形,
∴AF=CD.
∴![]() .
.
∴△ABE∽△ADC.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.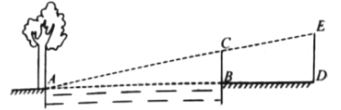
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB.分别交AC、BC于点E和点F,作PQ∥AC,交AB于点Q,连接QE.
中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB.分别交AC、BC于点E和点F,作PQ∥AC,交AB于点Q,连接QE.
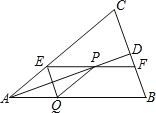
(1)求证:四边形AEPQ为菱形:
(2)当点P在线段EF上的什么位置时,菱形AEPQ的面积为四边形EFBQ面积的一半?请说明理
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°
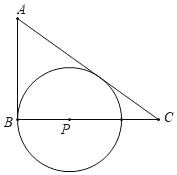
(1)在BC边上找一点P,作⊙P与AC,AB边都相切,与AC的切点为Q;(尺规作图,保留作图痕迹)
(2)若AB=4,AC=6,求第(1)题中所作圆的半径;
(3)连接BQ,第(2)题中的条件不变,求cos∠CBQ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点
上的一个动点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)如图①,求证:![]() ;
;
(2)如图②,连接![]() 为
为![]() 的中点,
的中点,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 和
和![]() 的长;
的长;
(3)如图③,过点![]() 作
作![]() 于
于![]() ,当
,当![]() 时,求
时,求![]() 的面积.
的面积.
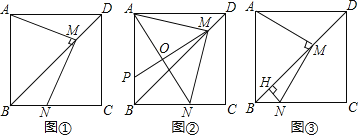
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两转盘分别标有数字。转盘一被三等分,转盘二被分成六份,其中标有数字“8的扇形的圆心角为90°,转动转盘,等旋转停止时,每个转盘上的箭头各指向一个数字(若箭头指向两个扇形的交线,则重新转动转盘,直到指向数字为止).
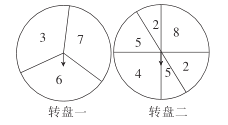
(1)转动转盘一一次,求出指向数字“3”的概率.
(2)同时转动两个转盘,通过画树状图法或列表法求这两个转盘转出的数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=120°,以BC为边向外作等边△BCD.
(Ⅰ)∠ABD+∠ACD=_____.
(Ⅱ)∠BAD=_____.
(Ⅲ)若AB=3,AC=2,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字0,1,2,3,B布袋中有三个除标号外完全相同的小球,小球上分别标有数字0,1,2.小明先从A布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.
(1)若用(m,n)表示小明取球时m与n 的对应值,用列表法(或画树状图)表示出(m,n)的所有取值;
(2)求关于x的一元二次方程![]() 有实数根的概率.
有实数根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com