
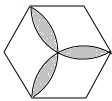
 向如图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
向如图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )| A. | $\frac{2\sqrt{3}-π}{π}$ | B. | $\frac{2π\sqrt{3}-9}{9}$ | C. | $\frac{π-\sqrt{3}}{π}$ | D. | $\frac{π\sqrt{3}-4}{9}$ |
分析 根据已知假设出六边形边长为1,进而求出正六边形面积和S扇形FAB,S扇形BCD,S扇形DEF,再利用三个扇形面积减去正六边形面积等于阴影部分面积,进而得出飞镖插在阴影区域的概率.
解答 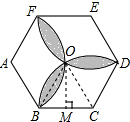 解:根据图象可以知,O为正六边形中心,过点O作OM⊥BC,
解:根据图象可以知,O为正六边形中心,过点O作OM⊥BC,
设正六边形边长为1,根据正六边形每个内角为120°,
则S扇形FAB=$\frac{120π×{1}^{2}}{360}$=$\frac{π}{3}$,
∴S扇形BCD=$\frac{120π×{1}^{2}}{360}$=$\frac{π}{3}$,S扇形DEF=$\frac{120π×{1}^{2}}{360}$=$\frac{π}{3}$,
∵OC=BC=BO=1,OM⊥BC,
∴OM=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
∴S△OBC=$\frac{1}{2}$×OM×BC=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$×1=$\frac{\sqrt{3}}{4}$,
∴S正六边形面积=$\frac{\sqrt{3}}{4}$×6=$\frac{3\sqrt{3}}{2}$,
∴S阴影=π-$\frac{3-\sqrt{3}}{2}$,
∴飞镖插在阴影区域的概率为:$\frac{π-\frac{3\sqrt{3}}{2}}{\frac{3\sqrt{3}}{2}}$=$\frac{2\sqrt{3}π}{9}$-1=$\frac{2\sqrt{3}π-9}{9}$;
故选B.
点评 此题主要考查了概率公式以及正六边形面积求法和扇形面积公式等知识,根据已知得出三个扇形面积减去正六边形面积等于阴影部分面积是解题关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
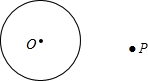 我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)
我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
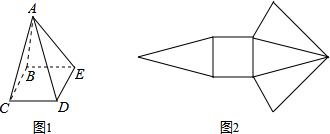
| A. | AC、AD、BC、DE | B. | AB、BE、DE、CD | C. | AC、BC、AE、DE | D. | AC、AD、AE、BC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com